Туннельный эффект (холодная эмиссия электронов и контактная разность потенциалов)

(3.1)

Отсюда видно, что доля каждого свободного электрона в общей теплоемкости такая же, как и свободного атома

Это противоречит экспериментальным фактам, согласно которым теплоемкость одноатомного металла определяется лишь теплоемкостью атомов решетки

, т. е. свободные электроны в первом приближении никакого вклада в теплоемкость металла не вносят.

Это противоречие было разрешено Зоммерфельдом, который показал, что к электронам в металле необходимо применять не классическую статистику с функцией распределения

а квантовую статистику Ферми – Дирака с функцией распределения

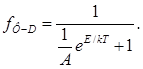
В основе квантовой статистики Ферми—Дирака лежит принцип Паули, согласно которому на каждом энергетическом уровне может находиться максимум два электрона (два квантовых состояния, отличающихся направлениями спинов).

Если нам задана трехмерная потенциальная яма кубической формы с длиной стороны, равной L, то составляющие импульса p =ђk будут связаны с целыми числами n1, n2, nз, характеризующими энергетический уровень, соотношениями:

Учтем, что на единичный интервал квантовых чисел:

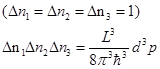(3.2)

приходится лишь один уровень, на котором могут находиться два электрона.

Поэтому если в единице объема находится ρо электронов, то максимальный импульс, которым может обладать электрон при абсолютном нуле температуры (T=0), определяется из соотношения

(3.3)

Или (3.4)

Соответствующая максимальная кинетическая энергия электронов равна:

(3.5)

Эта максимальная энергия при T= 0 соответствует уровню Ферми. Оценим значение этой энергии, например, для серебра. Плотность серебра равна 10,5, атомный вес 107,9. Считая, что число свободных электронов равно числу атомов серебра в единице объема, имеем:

Здесь мы использовали число Авогадро, т. е. число атомов в одном грамм-атоме, равное 6,02·1023. Отсюда по формуле (3.5) находим, что

Поскольку для серебра работа выхода W=3,7 эВ, то глубина потенциальной ямы в серебре оказывается равной 9,8 эВ. Схема заполнения электронных уровней в металле изображена на рис 3.1.

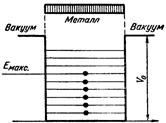
рис 3.1 Модель потенциальной ямы для металла. (Е макс. – верхняя граница заполненных уровней при Т=0 (энергия Ферми).

Средняя энергия в металле будет определяться выражением

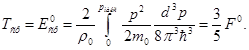(3.6)

Отсюда видно, что при сравнительно низких температурах электронный газ никакого вклада в теплоемкость не должен вносить, так как

Исходя из этой модели (рис 3.1), мы видим, что для вырывания электрона из металла необходимо сообщить ему энергию не меньшую, чем работа выхода

(3.7)

Как известно, в случае внешнего фотоэффекта электрон получает от поглощенного фотона энергию ђω. При этом электрон может покинуть металл, обладая кинетической энергией.

(3.8)

(уравнение Эйнштейна). Отсюда следует, что работа выхода есть минимальная энергия, которую нужно затратить, чтобы энергия электрона стала больше высоты потенциального барьера.

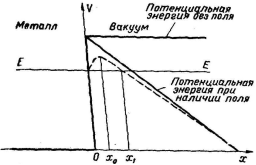
рис 3.2 Потенциальная энергия электрона в металле без поля и при наличии внешнего электрического поля. (штриховой линией показан ход потенциальной кривой с учетом сил электростатического изображения)

Если электроны в металле (электронный газ) имеют температуру выше абсолютного нуля, то часть электронов заполняет энергетические уровни выше уровня Ферми. Если увеличить кинетическую энергию электронного газа путем нагревания металла, то некоторая часть электронов может иметь энергию, превышающую энергию потенциального барьера, благодаря чему возникает ток из металла. Это явление, получившее название термоэлектронной эмиссии, используется, в частности для получения пучка электронов в электронных лампах. Однако возникновение тока электронов возможно и при низких температурах под влиянием постоянного внешнего электрического поля напряженности ξ, приложенного к поверхности проводника и направленного против оси –х. В этом случае потенциальная энергия электрона заряда -е0 равна (рис 3.2):

(3.9)

Помимо внешнего электрического поля, на электрон действует так называемая сила электрического изображения. Дело в том, что электрон, обладая зарядом —eо, создает на поверхности металла индуцированный заряд eо (рис 3.3).

Таким образом, полная сила, действующая на электрон, равна

(3.10)

Эффективная потенциальная энергия, учитывающая силы электрического изображения, равна:

(3.11)

Величина Vэфф имеет максимум в точке x0:

(3.12)

причем максимальное значение Vэфф меньше У0, так как

(3.13)

Учет сил электрического изображения показывает, что при наложении внешнего поля работа выхода уменьшается и становится равной

(3.14)

Однако силы электрического изображения не в состоянии объяснить холодную эмиссию. Действительно, оценка максимального тока (при W=0) приводит, например, для вольфрама к значению

(3.15)

между тем как на опыте достаточно сильный ток появляется уже при поле Е@4·106 в/см (Малликен).

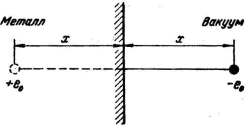
рис 3.3 Силы электрического изображения: на находящийся вне металла электрон действуют силы притяжения индуцированным зарядом.

 Скачать реферат