Туннельный эффект (холодная эмиссия электронов и контактная разность потенциалов)

§ 2. Кажущаяся парадоксальность «туннельного эффекта»

Прохождение частиц через потенциальные барьеры представляется на первый взгляд парадоксальным. Эту парадоксальность усматривают в том, что частица, находящаяся внутри потенциального барьера при полной энергии Е, меньшей высоты барьера V0, должна иметь отрицательную кинетическую энергию , и полная энергия, как это имеет место в классической механике, является суммой энергий кинетической и потенциальной:

В области, где, V >Е, это бессмысленно, так как импульс есть действительная величина. Как раз эти области, как мы знаем из классической механики, недоступны для частицы. Между тем, согласно квантовой механике, частица может быть обнаружена и в этой «запретной» области. Таким образом, получается, будто квантовая механика приводит к выводу, что кинетическая энергия частицы может быть отрицательной, а импульс частицы мнимым. Этот вывод и называют парадоксом «туннельного эффекта».

На самом деле здесь нет никакого парадокса, а сам вывод неверен. Дело в том, что, поскольку туннельный эффект есть явление квантовое (при ħ → 0 коэффициент прозрачности D (1.8) стремится к нулю), постольку он может обсуждаться лишь в рамках квантовой механики. Полную же энергию частицы можно рассматривать как сумму кинетической и потенциальной энергий только на основе классической механики. Формула предполагает, что одновременно знаем величину как кинетической энергии Т, так и потенциальной V. Иными словами, мы приписываем одновременно определенное значение координате частицы х и ее импульсу р, что противоречит квантовой механике. Деление полной энергии на потенциальную и кинетическую в квантовой механике лишено смысла, а вместе с тем несостоятелен и парадокс, основанный на возможности представить полную энергию Е как сумму кинетической энергии (функция импульса) и потенциальной энергии (функция координат).

Остается лишь посмотреть, не может ли все же оказаться так, что путем измерения положения частицы мы обнаружим ее внутри потенциального барьера, в то время как ее полная энергия меньше высоты барьера.

Обнаружить частицу внутри барьера действительно можно, даже если E<V; однако если фиксируется координата частицы х, при этом создается, согласно соотношению неопределенности, дополнительная дисперсия в импульсе так что уже нельзя утверждать, что энергия частицы, после того как определили ее положение, равна Е.

Из формулы для коэффициента прозрачности следует, что частицы проникают заметным образом лишь на глубину. Чтобы обнаружить частицу внутри барьера, мы должны фиксировать ее координату с точностью ∆x < l. Но тогда неизбежно возникает дисперсия импульса:

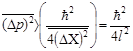
Подставляя сюда l2, находим

(2.1)

т. е. изменение кинетической энергии частицы, вносимое вмешательством измерения, должно быть больше той энергии, которой ей недостает до высоты барьера V0. Приведем еще пример, иллюстрирующий это утверждение. Определить координату частицы, находящейся внутри потенциального барьера таким путем, что будем посылать - узкий пучок света в направлении, перпендикулярном к направлению движения частицы. Если пучок рассеется, то значит, на его пути попалась частица.

Как объяснялось выше, точность нашего измерения должна быть такова ∆X<l; с другой стороны, нельзя создать пучок света, ширина которого была бы меньше длины световой волны λ, а, следовательно, длина волны света должна быть меньше l, т. е.

(2.2)

так как , где ω - частота световых колебаний, а с - скорость света, то отсюда следует, что

Встречающиеся в нерелятивистской механике энергии должны быть меньше собственной, энергии частицы mс2, поэтому

(2.3)

т. е. энергия применяемых в световом пучке квантов света должна быть больше, нежели разность между высотой потенциального барьера и энергией частицы. Таким образом, этот пример иллюстрирует положение о необходимости применить для измерения координаты приборы, обладающие достаточно большой энергией, чтобы можно было локализовать частицу.

§ 3. Вырывание электронов из металла. Холодная эмиссия

Теория туннельного эффекта имеет ряд весьма важных приложений в теории металлов и в ядерной физике. С помощью этой теории удалось понять ряд явлений, которые не нашли своего объяснения в классической физике. К числу этих явлений следует в первую очередь отнести холодную эмиссию, т. е. вырывание электронов из металла под действием электрического поля, а также возникновение контактной разности потенциалов. Однако прежде всего скажем несколько слов о теории «электронного газа», лежащей в основе электронной теории проводимости металлов.

Высокая электропроводность металлов говорит о том, что электроны способны сравнительно свободно перемещаться внутри всей кристаллической решетки металла. Затруднен лишь их выход из металла в вакуум, требующий затраты некоторой энергии, так называемой работы выхода. Это наводит на мысль рассматривать простейшую модель металла как свободный электронный газ, движущийся в потенциальной яме, внутри которой (т. е. в металле) потенциальная энергия равна нулю V=0, а вне, т. е. в вакууме, V=Vо>0.

Подобная упрощенная модель позволяет уяснить многие явления в металлах и поэтому в некоторых пределах является вполне разумной. Она была введена еще в классической теории (теория Друде, Лоренца и т. д.). В этом случае к электронам применялась классическая статистика Максвелла—Больцмана, которая до этого с успехом объяснила многие явления кинетической теории газов.

Однако в классической теории модель «электронного газа» встретила большие затруднения при построении теории теплоемкости. В самом деле, согласно известной теореме классической статистической механики о равномерном распределении энергии по степеням свободы на одну степень свободы в среднем должна приходиться энергия:

 Скачать реферат