Амплитудная модуляция и фазовое рассогласование магнитных сверхструктур

Рефераты / Физика и энергетика / Амплитудная модуляция и фазовое рассогласование магнитных сверхструктур

I ~ exp (-Whkl/kT) , (3)

где k – постоянная Больцмана; Т – абсолютная температура. Очевидно, что с наибольшей скоростью будут образовываться те зародыши, для которых работа Whkl является наименьшей. Выражение для работы образования Whkl любого типа двумерного зародыша имеет следующий вид:

, (4)

где Вhkl и Сhkl – коэфф

ициенты, y0 – энергия связи (работа отрыва) атома с основой, z - заряд адиона, е – заряд электрона, h - перенапряжение.

Работа образования двумерного зародыша грани (10.0) на собственной подложке, т.е. на грани (10.0) ГПУ-решетки (так как в этом случае y0 = С10.0) определяется по формуле:

. (5)

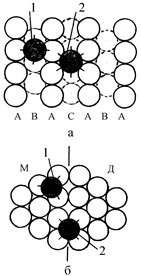
Коэффициент С10.0 характеризует энергию связи изолированного атома с основой, т.е. энергию связи атома, находящегося в нормальном положении на грани (10.0) (рис. 2 а, положение 1).

C10.0 = 4y1 + 4y2 + 7y4, (6)

где y1 и y2 и y4 –энергии связи между атомoм, находящимся на грани (10.0), и первыми, вторыми и четвертыми соседями, соответственно. Для кобальта y1 = 2.263×10-20Дж, y2 = 0.125y1, y3 = 0.0527y1, y4 = 0.01y1 [6].

На грани (10.0) в месте выхода ДУ энергия связи присоединяющегося атома с основой увеличивается, так как увеличивается количество соседей (рис. 2 а, положение 2).

= 6y1 + 2y2 + 8y4 . (7)

Подставив (4) и (5) в (2) получаем выражение для определения работы образования двумерного зародыша грани (10.0) в месте выхода ДУ на поверхности кристаллита:

. (8)

Из сопоставления уравнений (6) и (3) получаем, что < , и, согласно (1), можно сделать вывод, что в месте выхода ДУ скорость образования двумерных зародышей увеличивается и происходит преимущественный рост кристаллита. Поэтому поверхность кристаллита с ДУ становится полосчатой (ребристой).

Работа образования двумерного зародыша грани (00.1) на собственной подложке определяется по формуле, так как в этом случае y0 = C00.1 (см. формулу 2).

Энергия связи атома с основой, находящегося в нормальном положении на грани (00.1) (рис. 2 б, положение 1),определяется следующим образом:

C00.1 = 3y1 + 3y2 +y3+ 6y4. (8)

На грани (00.1) в месте выхода границы двойника выражение для энергии связи присоединяющегося атома с основой имеет другой вид (рис. 2 б, положение 2):

= 4y1 + y2 + 2y4 .

Рис. 2. Двумерные модели присоединения атома к граням ГПУ-решетки (10.0) (а) и (00.1) (б) в нормальное положение (1) и в месте выхода ДУ, положение (2) (а) и границы двойника, положение 2 (б). Грани (10.0) и (00.1) параллельны рисунку.

Подставив (8) и (9) в (2) получаем выражение для определения работы образования двумерного зародыша грани (00.1) в месте выхода границы двойника:

Из сопоставления уравнений (10) и (7) получим, что < , и, согласно (1), можно сделать вывод, что в месте выхода границы двойника образование двумерных зародышей облегчается. В ГПУ-решетке наиболее плотноупакованная грань (00.1) является и наиболее быстрорастущей в направлении <11.0> (в направлении самой плоскости) [5]. Так как структура двойника является зеркальным отражением структуры матрицы, в двойнике наиболее быстрорастущее направление <11.0> является также зеркальным отражением такого же направления в матрице. При формировании кристаллита с двойником эти направления и являются направлениями максимальной скорости роста. Так как вектора максимальных скоростей роста матрицы и двойника расположены под углом друг к другу, то равнодействующая их образуется путем геометрического сложения векторов и совпадает с плоскостью двойникования (рис.3). Расчет показывает, что скорость роста кристаллита, в котором ~50% двойников, в направлении плоскости двойникования может увеличиться до ~87%.Наличие смешанной текстуры [00.1]+[10.0] и неоднородной структуры поверхности пленок (рис.1б) подтверждают, что двойникование в осадках Co-W происходит в основном по граням (10.2) и (10.1). В этом случае более крупные кристаллиты, образовавшиеся в результате двойникования, вытянуты вдоль плоскостей двойникования (10.2) или (10.1).