Расчёт электромагнита клапанного типа
Определим сечение принятого провода с учётом изоляции [1, с.11]:
![]() мм2. ( 11 )
мм2. ( 11 )
Расчётное число витков обмотки при данном обмоточном окне и принятом проводе равно [1, с.12]:
![]() . ( 12 )
. ( 12 )
Округляя полученное число витков до сотен в большую сто
рону, принимаем:
![]() .
.
По найденному числу витков определим сопротивление обмотки [1, с.12]:
![]() Ом. ( 13 )
Ом. ( 13 )
Найдём значение расчётного тока катушки [1, с.12]:
![]() А. ( 14 )
А. ( 14 )
Для проверки правильности выполненного расчёта найдём намагничивающую силу разрабатываемой катушки и плотность тока, а так же нужно оценить тепловой режим [1, с.12]:
![]() А >
А >![]() А;
А;
![]() А/мм2 <
А/мм2 <![]() А/мм2.
А/мм2.
Тепловой режим катушки электромагнита характеризуется превышением температуры обмотки над температурой среды. Это превышение определяется по формуле [1, с.12]:
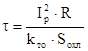 , ( 15 )
, ( 15 )
где kто – обобщённый коэффициент теплоотдачи;
Sохл – поверхность охлаждения катушки.
Величину коэффициента теплоотдачи можно определить по формуле [1, с.13]:
![]() , ( 16 )
, ( 16 )
где kто0 – коэффициент теплоотдачи при 0 ºС, kто0 = 1.4·10-5 Вт/(мм2·ºС);
β – коэффициент, учитывающий увеличение теплоотдачи при нагреве катушки, β = 5·10-8 Вт/(мм2·ºС);
tрасч – разность температуры окружающей среды и температуры нагрева обмотки, tрасч = 75ºС.
![]() Вт/(мм2·ºС).
Вт/(мм2·ºС).
Определим поверхность охлаждения катушки. Предположим, что материал каркаса имеет значительное тепловое сопротивление, существенно снижающее рассеяние тепла с торцевых и внутренней поверхностей катушки, тогда [1, с.13]:
![]() , ( 17 )
, ( 17 )
![]() мм2.
мм2.
Подставляя найденные величины в выражение ( 15 ) получим:
![]() ºС.
ºС.
Так как намагничивающая сила, получившаяся в результате проверки, больше заданной, плотность тока не превышает максимального значения и допускаемый нагрев катушки не превышает τдоп = 80 ºС, то расчёт проведён правильно.
4 Расчёт магнитной цепи методом коэффициентов рассеяния
Определение проводимости зазора
Используя метод Ротерса, разбиваем весь поток выпучивания на простые геометрические фигуры. Схема воздушного зазора представлена на рисунке 2.
Расчёт проводимостей производим для четырёх положений якоря электромагнита.
Якорь в отпущенном положении ( δ1 = δ1нач )
![]() , ( 18 )
, ( 18 )
![]() , ( 19 )
, ( 19 )
![]() , ( 20 )
, ( 20 )
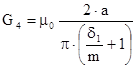 , ( 21 )
, ( 21 )
![]() , ( 22 )
, ( 22 )
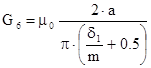 , ( 23 )
, ( 23 )
![]() , ( 24 )
, ( 24 )
![]() . ( 25 )
. ( 25 )
Подставляя в формулы ( 18 ) – ( 25 ) величину δ1 = δ1нач, определим проводимости для отпущенного положения якоря. Результаты вычисления приведены в таблице 2.
Якорь в промежуточном положении ( δ1 = ![]() δ1нач )
δ1нач )
Подставляя в формулы ( 18 ) – ( 25 ) величину δ1 = ![]() δ1нач, определим проводимости для отпущенного положения якоря. Результаты вычисления приведены в таблице 2.
δ1нач, определим проводимости для отпущенного положения якоря. Результаты вычисления приведены в таблице 2.
Якорь в промежуточном положении ( δ1 = ![]() δ1нач )
δ1нач )
Подставляя в формулы ( 18 ) – ( 25 ) величину δ1 = ![]() δ1нач, определим проводимости для отпущенного положения якоря. Результаты вычисления приведены в таблице 2.
δ1нач, определим проводимости для отпущенного положения якоря. Результаты вычисления приведены в таблице 2.
Якорь в притянутом положении ( δ1 = δ1кон )
Подставляя в формулы ( 18 ) – ( 25 ) величину δ1 = δ1кон, определим проводимости для отпущенного положения якоря. Результаты вычисления приведены в таблице 2.
Таблица 2 – Магнитные проводимости для четырёх положений
| δ1нач |
|
| δ1кон | |
| G1, Гн | 5.775·10-7 | 8.663·10-7 | 1.733·10-6 | 1.348·10-5 |
| G2, Гн | 1.046·10-8 | 1.046·10-8 | 1.046·10-8 | 1.046·10-8 |
| G3, Гн | 6.773·10-9 | 4.516·10-9 | 2.258·10-9 | 2.903·10-10 |
| G4, Гн | 9.309·10-9 | 1.182·10-8 | 1.617·10-8 | 2.381·10-8 |
| G5, Гн | 1.257·10-9 | 1.257·10-9 | 1.257·10-9 | 1.257·10-9 |
| G6, Гн | 1.138·10-8 | 1.536·10-8 | 2.363·10-8 | 4.452·10-8 |
| G7, Гн | 2.091·10-8 | 2.091·10-8 | 2.091·10-8 | 2.091·10-8 |
| Gδ1, Гн | 6.987·10-7 | 9.899·10-7 | 1.868·10-6 | 1.365·10-5 |
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода
