Пузыри в жидкости

.

Воспользуемся знанием величины в случае свободного всплывания пузырька и запишем нашу формулу в окончательном виде:

.

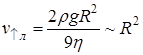Так как для воды вязкость , плотность , а ускорение свободного падения всегда , то скорость всплывания . Пузырек, радиус которого , всплывает медленно, со скоростью . Со дна до верха заполненного чайного стакана, высота которого , такой пузырек будет всплывать за время ! Так как , то пузырьки покрупнее всплывут за меньшее время.

Опыт по свободному всплыванию «маленького» пузырька в жидкости можно использовать для определения его размера, если известна вязкость жидкости.

Все наблюдали, что при сильном напоре воды в водопроводной системе, стакан наполняется молочно-белой водой, которая со временем просветляется. Мутность воды обусловлена огромным количеством взвешенных в ней газовых пузырьков, рассеивающих свет. А просветление воды наступает вследствие всплывания пузырьков, о чем убедительно свидетельствует появление именно у дна стакана расширяющегося просветленного слоя. Очень легко заметить, как со временем увеличивается ширина просветленного слоя. Располагая лишь часами и линейкой можно убедиться, что граница между мутной и прозрачной зоной движется с постоянной скоростью, и определить эту скорость.

Рисунок 2 Постепенное просветление стакана с газированной водой вследствие всплывания пузырьков

Этот опыт был проделан и найдено, что м/c. Согласно Стоксу, с такой скоростью должен всплывать пузырек, радиус которого м.

В совсем простом опыте со стаканом обычной воды, веря формуле Стокса, фактически измерили размер не видимого глазом пузырька. Ведь мы не видели отдельные пузырьки, а лишь наблюдали эффект рассеяния света множеством пузырьков и расширение у дна стакана прозрачного слоя воды, освободившегося от всплывших пузырьков.

Если захотим проверить, как формула Стокса согласуется с опытом, всякий раз наблюдая пузырек покрупнее, мы убедимся, что начиная с некоторых размеров сферических пузырьков формула Стокса начинает отказывать. Скажем, пузырек, радиус которого м, должен по Стоксу всплывать со скоростью м/с, а этого не происходит, он движется существенно медленнее.

Начиная с некоторой скорости всплывания могло бы оказаться, что при ламинарном обтекании жидкостью пузырька от его лобовой поверхности не будет успевать уводиться нужное количество жидкости. Тогда обязан объявиться иной характер движения жидкости, при котором быстрое перемещение пузырька станет возможным. Этот «иной характер» движения может оказаться следующим. От лобовой поверхности пузырька подгоняемая им жидкость перемещается быстро в направлении движущегося пузырька. В таком режиме движения жидкость в недостаточной степени затекает в «тыл» движущегося пузырька. И в его «тылу» могут возникнуть пустоты, разрывы, завихрения – все то, что в совокупности именуют «турбулентным» течением жидкости. На рис. 1 б) это изображено. В отличие от этого (рис. 1 а), на котором изображено ламинарное движение на рис. 1б линии искривляются, изображая вихри. Такому движению жидкости свойственна не упорядоченность вязкого течения, не взаимные соскальзывания соприкасающихся слоев жидкости, а образование завихрений в «тылу» движущегося пузырька. Упорядоченное вязкое течение сменяется вихревым, турбулентным.

Обсудим связь между выталкивающей силой и скоростью всплывания пузырька для случая, когда обнаружится второй турбулентный, характер движения жидкости у пузырька. Двигаясь со скоростью и пройдя путь l, пузырек передаст массе жидкости энергию

.

Эту энергию жидкость растратит на образование и движение завихрений. В конечном счете она превратится в тепло. Так как при равномерном движении

, то

.

Величину мы знаем и, следовательно, легко получим приближенную формулу, определяющую :

.

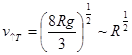Последнюю формулу можно было бы получить, пользуясь соображениями о размерностях.

Вывод: при свободном всплывании пузырька в режиме ламинарного течения воды , а в режиме турбулентного течения . Это означает, что с ростом скорости всплывания при турбулентном течении сопротивление жидкости движению пузырька увеличивается быстрее, чем при ламинарном.

Итак, скорость, при которой ламинарное обтекание пузырька жидкостью сменится турбулентным, можно оценить, приравняв силы, тормозящие пузырек, , и относящиеся к ламинарному и турбулентному течениям. Из такого сравнения следует, что если выполняется условие 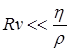, то пузырек всплывает в ламинарном режиме, а если 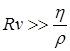- турбулентном. Для воды 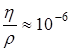м2/с, а для воздуха 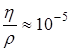м2/с. Пузырьки, имеющие радиус м, всплывают со скоростью м/с, т.е. м2/с, что существенно меньше, чем м2/с. Такие водяные пузыри всплывают «ламинарно». А мыльные пузыри, радиус которых м, падают со скоростью м/с. Значение м2/с существенно больше, чем 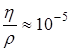м2/с и, следовательно, такие мыльные пузыри падают в турбулентном режиме.

 Скачать реферат