Пузыри в жидкости

.

Равенство растягивающего и сжимающего давлений, осуществляющееся в условиях равновесия, запишем следующей главной формулой:

, или .

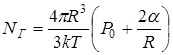Записанная формула и выражает интересующую нас связь

между NT и R.

Та внешняя сила, которой можно «щупать» пузырь для того, чтобы выяснить «мягкий» он или «твердый», определяется давлением Р0. Его можем изменять по собственному желанию. Если , то, изменяя (разумеется, не нарушая неравенства), мы никак не повлияем на размер пузыря, который сильно сжат собственным, лапласовским давлением, значительно большим, чем внешнее. То есть, если радиус пузыря настолько мал, что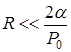— внешнее давление пренебрежимо мало по сравнению с лапласовским и поэтому до тех пор пока это неравенство сохраняется, пузырь сохранит свой радиус. А это и значит, что он твердый! А вот в случае, когда , лапласовское давление значительно меньше внешнего и поэтому любое давление будет приводить к изменению радиуса пузыря. Больше давление — меньше радиус, меньше давление — больше радиус. Это — «мягкий» пузырь, он чувствует внешнее давление. Увеличивая внешнее давление, его можно сжать.

Для того чтобы наши рассуждения обрели количественную меру, оценим радиус пузыря , который сжимается лапласовским давлением, равным внешнему . Такой пузырь является как бы пограничным между «мягкими» и «твердыми» пузырями. Если внешнее давление равно атмосферному, то

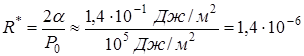м.

Итак, «твердые» пузыри в воде — это те, радиус которых значительно меньше микрометра, а «мягкие» — это те, радиус которых значительно больше микрометра.

«Мягкие» и «твердые» пузыри отличаются не только размерами. Оказывается, что во многих реальных ситуациях они обнаруживают различные свойства и различное поведение.

Для «мягкого» пузырька, когда лапласовским давлением можно пренебречь, из главной формулы следует . Это означает, что при объединении двух «мягких» пузырей будут суммироваться их объемы, так как суммируется число газовых молекул. Из этого обстоятельства проистекают два важных следствия.

Во-первых, оно означает, что объем образовавшегося пузыря равен сумме объемов объединившихся.

Во-вторых, оказывается, что два объединившихся пузыря имеют поверхность меньшую, чем та, которую они имели до объединения. Действительно, условие суммирования объемов двух пузырей, радиусы которых и , означает, что

.

Это равенство можно переписать в иной форме:

.

Так как , то

.

Именно в этом неравенстве и содержится энергетическое оправдание объединения «мягких» пузырей: энергия заключенного в них газа не меняется, а связанная с ними поверхностная энергия уменьшается. Так что в процессе слияния общая энергия уменьшается — слияние «мягких» пузырей энергетически выгодно.

Теперь о слиянии «твердых» пузырей. Для них из главной формулы следует . Это значит, что при слиянии таких пузырей суммируются не их объемы, а поверхности:

.

При этом объем суммарного пузыря должен превосходить сумму объемов слившихся пузырей:

.

Вывод: при слиянии «твердых» пузырей поверхность, а значит, и энергия поверхности, остаются неизменными. Казалось бы, и объединяться им нечего. Есть, однако, оправдание процесса слияния твердых пузырей. Оно заключается в том, что слиянию пузырей сопутствует расширение газа.

4. Газовый пузырек у границы между жидкостями

Газовый пузырек, проходящий через границу между жидкостями,— участник многих очень важных технологических процессов. Вот пример такого процесса. Для того чтобы выплавляемый металл был высококачественным, тщательно перемешанным, сквозь жидкий расплав пропускают пузырьки газа. Производят, как говорят металлурги, барботаж расплава. В виде пузырьков газ проходит и сквозь слой металла, и сквозь слой находящегося на нем жидкого шлака. А между слоями — граница, и пузырьки газа должны ее преодолеть. Для металлургов очень важно знать закономерности этого процесса.

Вначале попробуем представить себе судьбу газового пузырька радиуса R, расположенного в нижней жидкости вблизи границы между нижней и верхней жидкостями. Для облегчения нашей задачи упростим ее и предположим, что плотности жидкостей одинаковы и равны и, следовательно, выталкивающая сила от сорта жидкости не зависит. Предположим вначале, что граница между жидкостями остается плоской, когда пузырек пытается пройти сквозь нее. Жидкости отличаются коэффициентами поверхностного натяжения и , а граница между ними характеризуется коэффициентом поверхностного натяжения .

Газовый пузырек либо пройдет сквозь границу, либо задержится границей и останется на ней.

Судьба газового пузырька определится совместным действием трех сил. Перечислим и оценим эти силы. Одна из них — выталкивающая сила — обусловлена уменьшением потенциальной энергии всплывающего пузырька. Вторая сила обусловлена тем, что прохождению пузырька сквозь границу сопутствует исчезновение части поверхности границы и, следовательно, уменьшение энергии системы на значение произведения площади этой поверхности на . Третья сила определяется тем, что при движении пузырька через границу меняется соотношение между площадями поверхности пузырька, где коэффициенты поверхностного натяжения и различны. При этом, разумеется, изменяется поверхностная энергия, связанная со всей поверхностью пузырька .

 Скачать реферат