Постулаты квантовой механики

С учетом независимости пространственных и временных переменных следует обе части полученного равенства (2.23) приравнять одной и той же постоянной величине, в результате получим систему из двух уравнений:

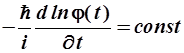(2.24)

(2.25)

Легко видеть, что выражение (2.2

5) имеет вид операторного уравнения (1.1) и, следовательно, постоянная const есть собственное значение гамильтониана, то есть энергия системы:.

Временная часть волновой функции φ(t), получаемая как решение уравнения (2.24), имеет вид строго периодического процесса, совершающеюся с круговой частотой, а именно:

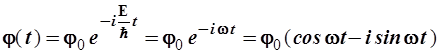(2.26)

Как уже говорилось ранее, временная периодичность функций состояния является неотъемлемой чертой стационарного движения. Операция комплексного сопря­жения уравнения (2.19) означает замену t на -t, т.е. время как бы обраща­ется вспять. Временная часть волновой функции в (2.26) обратится в физически эквивалентную , но любая наблюдаемая величина останется той же самой согласно (1.5). Уравнение Шрёдингера описывает, таким образом, процессы, обратимые во времени.

2.3.5. Наконец, из уравнения (1.25) для стационарных систем получаем операторное выражение закона сохранения энергии:

(2.27)

Это выражение называется стационарным уравнением Шрёдингера. Оно не содержит времени в явном виде. Стационарное уравнение Шрёдингера является основным инструментом для решения теоретических задач об электронном строении атомно-молекулярных систем. В процессе точного или приближенного решения уравнения (2.27) находится вид волновой функции, а также энергия исследуемых состояний.

2.3.6. Всякая система характеризуется своим гамильтонианом, и он является тем исходным общим условием, которое управляет и характером движения, и предписывает возможный вид состояний и уровней системы

2.4. Постулат 4. Принцип суперпозиции состояний

2.4.1. Если возможными волновыми функциями являются и то возможно такое состояние системы, которому отвечает волновая функция

(2.28)

2.4.2. Этот постулат математически оформляет связь между чистыми и смешанными состояниями квантово-механической системы, о которых говорилось в разделе 1. Образ смешанного состояния, согласно сформулированному утверждению, оказывается суперпозицией – наложением волновых функций чистых состояний, Отсюда данный постулат называется принципом суперпозиций.

Еслии принадлежат некоторому ортонормированному набору, т.е.

и ,

то формулу нормировки смешанного состояния (2.29) можно считать условием, определяющим вклады отдельных чистых состояний в смешанное:

(2.29)

Отсюда следует, что вероятность обнаружить систему в каком-либо из чистых состояний (1 или 2) в составе смешанного равна квадрату коэффициента (или соответственно).

2.5. Постулат 5. Средние значения динамических переменных

2.5.1. Среднее значение динамической переменной , получаемое из множества измерений, равно математическому ожиданию этой величины:

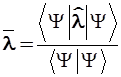(2.30)

Если волновая функция нормирована, то знаменатель единичен, и получаем более простое выражение;

(2.31)

2.5.2. Покажем, что у чистых состояний квантово-механической системы средние значения наблюдаемых переменных совпадают с собственными значениями соответствующих эрмитовых операторов. В этом случае формулы (2.30) и (2.31) непосредственно следуют из фундаментального операторного уравнения (1.1).

Чтобы показать это, запишем уравнение (1.1) с помощью символики Дирака, далее слева скалярно домножим каждую его часть на бра-вектор | и выделим в правой части равенства собственное число . В итоге приходим к формулам (2.30) и (2.31). Цепочка простейших преобразований имеет вид:

Для общего случая смешанных состояний подобного обоснования нет, и формулы (2.30) и (2.31) постулируются. Этот постулат приобретает уже универсальное содержание. С его помощью можно рассчитывать средние значения даже тех динамических переменных, операторы которых не обладают дискретными спектрами волновых функций и собственных значений, например, координаты и потенциальной энергии.

 Скачать реферат