Постулаты квантовой механики
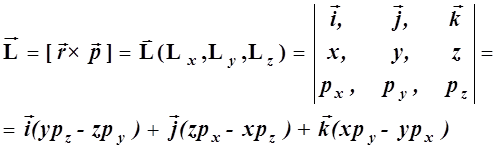 (2.5)
(2.5)
и, соответственно, его проекции равны
![]() (2.6)
(2.6)
![]() (2.7)
(2.7)
![]() (2.8
(2.8
- кинетическая энергия Т, скалярная вели
чина, которая в поступательном движении связана и с массой и импульсом
![]() ;
;
для одномерного вращения вокруг оси (например, z) справедлива подобная же формула, где масса заменена моментом инерции Iz, а импульс – его моментом ![]() :
:
![]()
- потенциальная энергия, т.е. скалярное силовое поле, задаваемое функци-ей координат ![]() , в котором движется частица;
, в котором движется частица;
- полная энергия Е, равная сумме кинетической и потенциальной энергий ![]()
2.2.3. С учетом общих требований, предъявляемых к операторам квинтовой механики, постулируются простейшие операторы, а именно: операторы координат, определяющие положение частицы, и импульса ее,
- оператор координаты ![]() совпадает с умножением на саму координату q, т.е.:
совпадает с умножением на саму координату q, т.е.: ![]() , или угол
, или угол![]() ,
,
или, в общем виде ![]() ;
;
- оператор импульса имеет дифференциальную форму
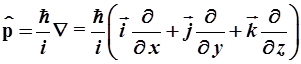 (2.9)
(2.9)
где постоянная Планка ![]() Дж·с,
Дж·с, ![]() и операторы координат импульса соответственно равны:
и операторы координат импульса соответственно равны:
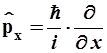 ,
, 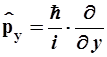 ,
, 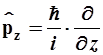 (2.10)
(2.10)
Введение в оператор, мнимой единицы превращает его в самосопряженный т.е. отвечающий условию (1.5).
2.2.4. Остальные операторы строятся по формулам классической механики, где вместо координат и импульсов используются их операторы, Это утверждение можно считать следствием макроскопического устройства приборов по законам классической физики. Построим операторы ![]() и
и ![]() для одной частицы:
для одной частицы:
- операторы момента импульса и его проекций:
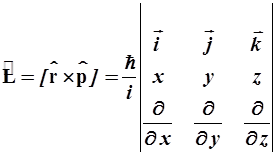 , (2.11)
, (2.11)
 , (2.12)
, (2.12)
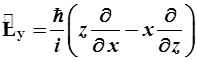 , (2.13)
, (2.13)
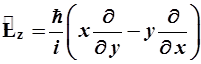 (2.14)
(2.14)
В полярных координатах (например, сферических) соответствующие производные декартовых координат ![]() следует заменить их выражениями через полярные переменные
следует заменить их выражениями через полярные переменные![]() ;
;
- оператор кинетической энергии в декартовых координатах:
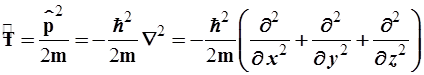 (2.15)
(2.15)
Переходя к полярным координатам, лапласиан ![]() преобразуют к ним. Для случая вращения по поверхности без радиальной компоненты движения, как это имеет место при вращении двухатомной молекулы вокруг центра масс, можно записать:
преобразуют к ним. Для случая вращения по поверхности без радиальной компоненты движения, как это имеет место при вращении двухатомной молекулы вокруг центра масс, можно записать:
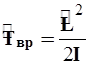 (2.16)
(2.16)
оператор потенциальной энергии, подобно координате, дается просто умножением на функцию потенциальной энергии, т.е.
![]() , или
, или ![]() (2.17)
(2.17)
оператор полной энергии называют гамильтонианом, в честь английского ученого Гамильтона, оставившего фундаментальные труды в механике, астрономии и математике, и обозначают его ![]()
![]() (2.18)
(2.18)
2.3. Постулат 3. Уравнение Шрёдингера
2.3.1. Эволюция системы определяется, с одной стороны, ее мгновенным состоянием и, следовательно, волновой функцией. С другой стороны, изменение состояния во времени зависит от "скорости" эволюции, т.е. от производной волновой функции по времени. Вместе с тем такое изменение связано с каким-либо взаимодействием с окружающими систему объектами и, следовательно, с обменом энергией. Это означает, что при описании эволюции необходимо связать саму волновую функцию, ее производную по времени ![]() и гамильтониан, в общем случае зависящий от координат и времени.
и гамильтониан, в общем случае зависящий от координат и времени.
2.3.2. Такая связь вводится в виде временнớго уравнения Шрёдингера, которое является одним из постулатов квантовой механики и записывается в форме:
 (2.19)
(2.19)
Возможные функции состояния системы ![]() удовлетворяют уравнению (2.19)
удовлетворяют уравнению (2.19)
2.3.3. В том случае, когда гамильтониан Н, а, следовательно, и энергия системы не зависят от времени, временное уравнение Шредингера легко преобразуется в стационарное уравнение Шредингера, имеющее структуру операторного уравнения (1.1).
Произведем соответствующие преобразования. Для этого положим, что гамильтониан не включает времени в явном виде и зависит только от координат
 (2.20.)
(2.20.)
Это позволяет нам использовать метод Фурье для разделения переменных и представить волновую функцию в виде двух сомножителей, одного покоординатного и другого временного:
![]() (2.21)
(2.21)
Подставим результат в (2.20) и перенесем ![]() влево от
влево от ![]() , а
, а ![]() влево от оператора дифференцирования по времени, так как по отношению к этим операторам выносимые множители условно постоянны и не преобразуются:
влево от оператора дифференцирования по времени, так как по отношению к этим операторам выносимые множители условно постоянны и не преобразуются:
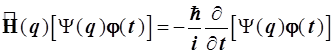 ,
,
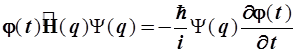 (2.22)
(2.22)
Теперь разделим переменные в уравнении (2.22)
 (2.23)
(2.23)
