Количественные методы в бизнесе

Кривые роста - это математические функции, предназначенные для аналитического выравнивания временного ряда.

Наиболее часто в практической работе используются кривые роста, которые позволяют описывать процессы трех основных типов: без предела роста; с пределом роста без точки перегиба; с пределом роста и точкой перегиба.

Для описания процессов без предела роста служат функции:

table border=0 cellspacing="0" cellpadding="0" align="center">

Y(t) = A0 + A1t

- прямая

Y(t) = A0 + A1t + A2t2

- парабола II порядка

Y(t) = exp(A0)tA1

- степенная

Y(t) = exp(A0 + A1t)

- экспонента

Y(t) = exp(A0 + A1t)tA2

- кинетическая кривая

Y(t) = A0 + A1Lnt (1+ A2Lnt)

- линейно-логарифмическая функция II порядка

Y(t) = A0 + A1Ln(t)

- линейно -логарифмическая функция I порядка

Процессы развития такого типа характерны в основном для абсолютных объемных показателей, но часто им соответствует и развитие некоторых качественных относительных показателей.

Основной подход выделения сезонной компоненты основан на предварительном сглаживании данных и выделении тенденции при помощи скользящей средней (на нем базируются статистические критерии сезонности: дисперсионный, автокорреляционный, гармонический и др.). Наиболее распространен гармонический критерий, который позволяет не только проверять наличие сезонных колебаний, но и оценивать значимость гармоник Фурье, отображающих эти колебания.

Достоинство таких моделей состоит в том, что они обеспечивают стабильность прогноза даже в точках цикла с наименьшими значениями прогнозируемой переменной.

Для прогнозирования сезонных процессов используются модели трех типов: СС - модели (скользящего среднего); АР - модели (авторегрессии); и АРИСС - модели (смешанные модели интегрированного скользящего среднего). Модели последнего класса обычно реализуются по методике Бокса- Дженкинса. Они, как и многие другие сложные с теоретической и практической точки зрения средства статистического анализа. требуют индивидуального подхода к исследуемому показателю и высокой квалификации исследователя. Поэтому в практике массовых статистических расчетов обычно используются модели первых двух классов.

Сезонные колебания могут быть отражены СС-моделями двух типов мультипликативной и аддитивной [8,14].

Сезонные компоненты, по природе своей, могут быть аддитивными или мультипликативными. Различие между двумя видами сезонности состоит в том, что в аддитивной модели сезонные отклонения не зависят от значений ряда, тогда как в мультипликативной модели величина сезонных отклонений зависит от значений временного ряда.

2. Расчет параметров функции долговременного тренда T(t) обычно производится методом наименьших квадратов (МНК). В качестве решения принимается точка минимума суммы квадратов отклонений между теоретическим и эмпирическим уровнями:

где: yt2 - выровненные (расчетные) уровни;

yt- фактические уровни.

Параметры уравнения ai, удовлетворяющие этому условию, могут быть найдены решением системы нормальных уравнений. На основе найденного уравнения тренда вычисляются выровненные уровни. Нормальные уравнения МНК имеют вид:

для линейного тренда:

Рис. 1.1 - Поиск долговременного линейного тренда и оценка наличия сезонной функции в остаточных членах отклонения факта от линейного прогноза

Для решения указанного уравнения используют встроенные функции анализа пакета «электронных таблиц» EXCEL-2000. На рис. 1.1 приведены результаты определения долговременного линейного тренда фактической функции прибыли за 10 кварталов.

Как видно из графиков рис. 1.1 остаточные члены имеют устойчивую гармоническую составляющую с периодом 2 квартала и снижением амплитуды гармоник по времени.

Рис. 1.2 - Определение функции, описывающей изменение амплитуды гармоник

Для оценки функции снижения амплитуды гармоник проведем статистическую обработку модулей отклонений фактической прибыли от линейного прогноза в среде «электронных таблиц» EXCEL-2000 (рис.1.2).

Учитывая данные, приведенные на рис. 1.1, 1.2 полученные регрессионные уравнения следует отнести к устойчивым, поскольку показатель отклонения

R2 > 0,6.

Таким образом:

- полученное уравнение линейной регрессии:

Y=-10,6*x+144,2

- полученное уравнение мультипликативной регрессии с сезонным компонентом:

Y= -10,6*x+144,2+(-1,0909*x+15,2)*cos[3,1416*(x-1)]

На рис. 1.3 приведены результаты прогнозирования:

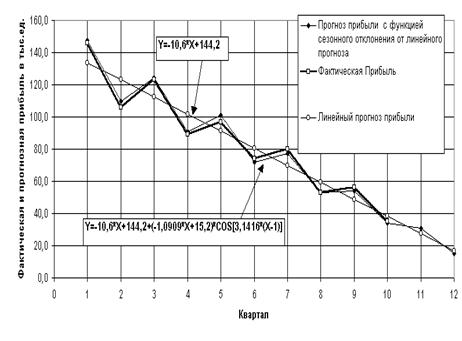
Рис. 1.3 - Результаты прогнозирования фактической прибыли уравнением мультипликативной регрессии с сезонным компонентом (гармоника с периодом в 2 квартала)

В табл. 1.1 представлены результаты расчета – прогнозирования прибыли предприятия в 11 и 12 квартале (3 и 4 квартал 3 года работы предприятия) с использованием уравнения мультипликативной регрессии с сезонным компонентом гармоники.

На рис. 1.4 представлены результаты оценки остаточных членов компоненты E(t).

Таблица 1.1 - Результаты прогнозного моделирования

Рис. 1.4 - Оценка членов остаточной компоненты уравнения моделирования

2. Сетевой анализ и планирование проектов

В таблице ниже приведен перечень мероприятий по расширению производства в связи с открытием второго завода. Программой расширения предусматривается перевод персонала с существующего завода (завод А) на новый завод (завод Б). Далее приведены детали этой программы, в том числе обычная продолжительность и расходы, а также сокращенная продолжительность и соответствующие расходы по каждому действию:

 Скачать реферат