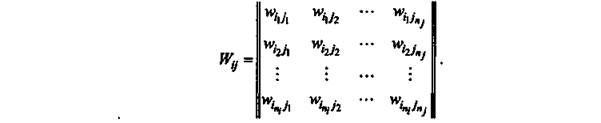Теория систем

Многообразие математических задач, сопутствующих реализации метода анализа иерархий, реализовано в системе поддержки принятия решений Expert Decide, версии 2.0 и 2.2. Основные функции, а также приемы работы в данной системе описаны в Руководстве пользователя.

Иерархический синтез в случае моделей, содержащих более трех уровней, следует проводить с помощью математического пакета MathCAD, исп

ользуя матричные вычисления.

2. Метод аналитических сетей

Метод аналитических сетей (МАС) является обобщением МАИ на случай, когда взаимодействием иерархических уровней (компонентов) и/или их элементов нельзя пренебречь. Многие проблемы принятия решений нельзя представить иерархическими структурами, потому что в них существуют зависимости и взаимодействия между элементами разных уровней иерархии. Часто возникают задачи, в которых не только важность критериев влияет на приоритеты альтернатив (как в иерархиях), но также важность альтернатив влияет на приоритеты критериев. Не всегда можно говорить и об альтернативах в прямом смысле этого слова. Так, при оценке мероприятий по инновационному развитию фирмы различные направления этого развития уже не являются чисто альтернативными и могут реализовываться одновременно (так называемые "мультипроекты"), хотя и с различной интенсивностью. Взаимодействовать могут также и критерии оценки альтернатив.

Решения, полученные на сети, могут отличаться от решений, полученных даже на сложной иерархии. Далеко не всегда искусственное преодоление сложности путем сведения реальной задачи к простой структуре позволит получить результат взаимодействия между элементами проблемы в форме обобщенных суждений, правильно отражающих действительность. Поэтому важно представлять эти суждения такими структурами, которые адекватно отражают реальность.

Главное преимущество сетей с обратными связями – возможность получения решений, которые позволяют предвидеть будущее.

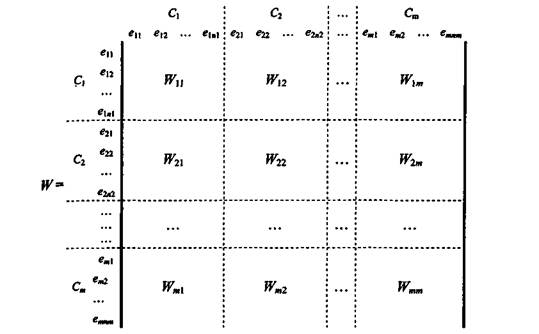
Центральное понятие в МАС – суперматрица (рисунок 1).

Элементы Wij в суперматрице являются блоками (компонентами) и представляются матрицами – рисунок 2.

Каждый столбец в матрице Wij являются главным собственным вектором влияния элементов i-го компонента сети на элементы j-го компонента, при этом нулевые элементы вектора соответствуют элементам, не оказывающим влияния на другие элементы блока.

В общем случае сеть рассматривается как система и состоит из компонентов и элементов, которые содержатся в этих компонентах. Влияния, которые оказывают элементы некоторого компонента на другие элементы в системе, представляются векторами приоритетов, полученными на основе парных сравнений (как в МАИ). Взаимные влияния элементов в сети представляются в виде суперматрицы, блоками которой являются матрицы Wij традиционного в МАИ вида, т.е. каждый столбец в матрице Wij представляет собой главный собственный вектор влияния элементов i-го компонента сети на элементы j-го компонента. Но, в отличие от МАИ, в матрице Wij элементам, не оказывающим влияния, соответствуют нулевые элементы вектора. При парных сравнениях используются только те элементы компонента, которые имеют влияние. Если на нижнем уровне иерархии каждый элемент зависит только от самого себя, то в суперматрицу вводится блок, состоящий из нулей (иногда – единичная матрица; результат будет идентичным).

Сеть можно получить из иерархии, постепенно увеличивая количество учитываемых внешних и внутренних связей между элементами. В общем случае сеть состоит из компонентов и элементов, которые содержатся в этих компонентах. Но при создании структур для моделирования проблем могут использоваться совокупности компонентов – подсистемы. В порядке уменьшения размера выделяют: собственно систему, состоящую из подсистем; подсистемы, состоящие из компонентов; компоненты, содержащие множества элементов.

В ряде случаев удается "разбить" сложную проблему, требующую применения методологии аналитических сетей, на несколько подпроблем, решение которых может быть достигнуто с помощью более простого и, главное, более наглядного метода аналитических иерархий. Учет же взаимодействий или обратных связей при этом производится на меньшем числе компонентов сетей, что позволяет снизить размерность суперматриц. В этом случае для решения подпроблем можно использовать экспертно-аналитическую систему Expert Decide, а операции с суперматрицами проводить в математической системе MathCAD.

3. Постановка задачи

В данной курсовой работе рассматривается модель оценки приоритетов акторов в развитии поствузовского образования в орловском регионе.

Элементы модели организованы в иерархическую структуру с уровнями (рис. 3):

Рис.3 - Иерархическая модель факторов, акторов и альтернатив путей развития поствузовского образования в орловском регионе.

Поясним уровни и элементы иерархии:

· верхний уровень содержит цель (фокус) – будущее поствузовского образования.

· второй уровень –первичные факторы: экономические, политические, социальные, технологические, потребность рынка;

· третий уровень – акторы: аспиранты, профессорско-преподавательский состав, администрация вуза, местные власти, центральные власти, экономика;

· четвертый уровень – альтернативные сценарии: образование для подготовки научных кадров, подготовка преподавательских кадров, подготовка кадров для экономики.

Приведенная на рис.3 иерархическая модель предоставляет достаточно большие аналитические возможности. Она не только обеспечивает выявление весов критериев и взвешенных по этим весам приоритетов альтернативных сценариев развития поствузовского образования, что является основной задачей экспертно-аналитического моделирования, но предоставляет также дополнительные возможности:

1) выявление наиболее значимых показателей, что позволяет существенно сократить размерность матриц парных сравнений на следующем уровне, следовательно, приводит к уменьшению объема работы экспертов;

2) выявление наиболее значимых политик акторов.

Хотя с помощью данной иерархической модели, в основном, фиксируется существующая ситуация, тем не менее, модель направлена в будущее.

Определенным недостатком описанной выше иерархической модели является неучет взаимодействия акторов. Следовательно, помимо модели прямой иерархической зависимости, необходимо рассмотреть также сетевую модель (рис.4):

 Скачать реферат