Интеллектуальные компьютерные технологии защиты информации

Доказано, что сходимость этой процедуры обеспечивается практически во всех случаях.

Заметим, однако, что приведенная рекуррентная процедура справедлива лишь для случая нормированных оценок группы взаимооцениваемых элементов. В случае же ненормированных оценок или независимого оценивания отдельных элементов групповая оцен

ка может быть вычислена по такой (тоже рекуррентной) процедуре:

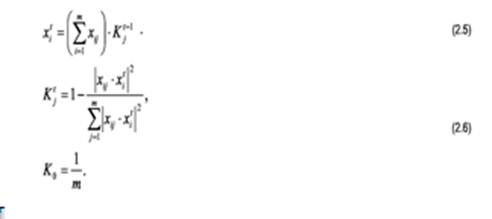
Нетрудно видеть, что в данном случае может быть построена рекуррентная процедура аналогично тому, как это представлено выше в п. «б».

д) Оценки экспертов осуществляются в лингвистическом выражении. Как показано в табл. 2.1, в данном случае могут быть получены две групповые оценки: лингвистические значения оцениваемых элементов и/или количественная оценка.

Лингвистические оценки могут быть получены процедурой «голосования», т.е. выбором того значения, которое дано большинством экспертов. Для элементов повышенной значимости может быть использовано правило квалифицированного большинства ("за» - не менее 75% оценок экспертов).

Количественная групповая оценка по совокупности оценок лингвистических может быть определена следующим образом. Пусть, например, каждому эксперту предлагается дать лингвистическую оценку требуемого уровня защиты информации на конкретном объекте одним из следующих значений: 1) не нужна; 2) невысокая, 3) средняя, 4) высокая, 5) очень высокая. Кроме этого, каждый эксперт приводит тот диапазон на шкале 0-1, в котором, по его мнению, находится его оценка. Тогда в качестве количественной его оценки может быть принята середина указанного интервала, а затем оценки всех экспертов могут быть обработаны по методике, рассмотренной в п. «б».

Такая лингвистико-количественная экспертиза особенно целесообразна в тех случаях, когда оценке подвергается сложное многофакторное событие с высоким уровнем неопределенности.

2.3.4 Неформальные методы поиска оптимальных решений

Решение проблем защиты информации связано с поиском оптимальных решений, т.е. таких вариантов действий, которые при заданных затратах ресурсов обеспечивают максимальную эффективность процессов или достижение заданной эффективности процессов при минимальных затратах ресурсов.

Процедуры поиска оптимальных решений являются наиболее сложными процедурами, осуществляемыми при создании, организации и обеспечении функционирования больших систем, поэтому разработке методологии поиска оптимальных решений в различных ситуациях уделяется повышенное внимание. К настоящему времени разработан достаточно представительный арсенал методов поиска оптимальных решений в самых различных ситуациях. Практическая реализация подавляющего большинства методов сопряжена с осуществлением значительного объема сложных расчетов, поэтому регулярное и интенсивное их развитие началось лишь после появления ЭВМ. Вполне естественно поэтому, что развивались главным образом те методы, которые могли быть реализованы конечными алгоритмами. Данному условию отвечают далеко не все методы, а те, которые ему отвечают, позволяют решать далеко не все оптимизационные задачи, с которыми приходится встречаться на практике. Особенно трудными для реализации являются те задачи, в постановке которых имеются неопределенности. А именно такие задачи возникают при решении проблем защиты информации в КИС. В связи с этим особый интерес представляют развиваемые в последние годы неформальные методы поиска оптимальных решений. При этом обозначилось два направления использования неформальных методов в решении оптимизационных задач:

• сведение сложной неформальной задачи к формальной постановке в целях использования уже реализованных формальных методов;

• неформальный поиск оптимального решения, т.е. непосредственная реализация процедуры поиска.

Классификационная структура методов приведена на рис. 2.2.

Сведение неформальной задачи к формальной постановке заключается в формировании строго выраженных условий задачи, т.е. подлежащих поиску Переменных, ограничений, которым должны удовлетворять переменные, и целевой функции, подлежащей максимизации или минимизации в процессе поиска оптимального решения. Для этих целей, как показано на рисунке, могут использоваться методы теории нечетких множеств, эвристическое программирование и эволюционное моделирование.

Методы теории нечетких множеств позволяют получать аналитические выражения для количественных оценок нечетких условий принадлежности элементов к тому или иному множеству и тем самым сводить постановки неопределенных задач к строго определенным. При наличии же строгих постановок для решения задачи могут быть использованы соответствующие конечные методы, которые, как известно, гарантируют поиск оптимальных решений.

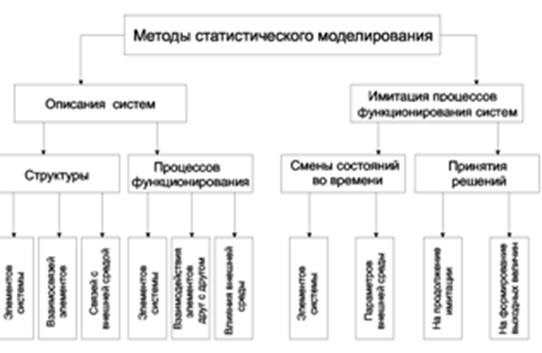
Рис. 2.2. Классификационная структура методов поиска оптимальных решений

Эвристическим программированием названы такие методы поиска оптимальных решений, основу которых составляют формализованные (т.е. представленные в виде конечного алгоритма) эвристики. Под эвристикой (эвристическим правилом, эвристическим методом) принято понимать правило, стратегию или просто ловкий прием, найденные человеком на основе своего опыта, имеющихся знаний и интуиции, и позволяющие наиболее эффективно решать некоторый класс слабоструктурированных задач. Найденные таким образом эвристики подвергаются формализации с целью представления их в виде конечного алгоритма, который можно реализовать на ЭВМ.

Таким образом, схема разработки методов эвристического программирования в обобщенном виде может быть представлена следующей последовательностью процедур: изучение содержания соответствующего класса слабоструктурированных задач; изучение приемов решения задач данного класса человеком; выявление закономерностей в решении человеком задач рассматриваемого класса; формализация выявленных закономерностей, приемов и правил и построение на этой основе модели решения задач данного класса; алгоритмическая реализация построенной модели.

Принципиальным моментом является то, что методы эвристического программирования вовсе не гарантируют получения строго оптимальных решений. Более того, не исключаются даже случаи, когда полученное на основе эвристической модели решение будет далеко от оптимального. Единственное, что гарантируют эти методы - это, во-первых, что решение непременно будет найдено, и, во-вторых, что найденное решение будет лучшим среди решений, получаемых без использования эвристик.

Регулярная теория построения эвристических моделей до настоящего времени в полной мере не разработана. Наиболее правдоподобной представляется следующая интерпретация принципиальных отличий эвристического поиска от поиска по конечным формальным методам. В процессе решения задачи строго формальными методами поле поиска (область допустимых решений) остается неизменным. Сам процесс решения заключается в прямом, направленном или случайном переборе возможных решений. Для эвристических же методов характерно, с одной стороны, сужение поля поиска (области допустимых решений) за счет исключения из рассмотрения подобластей заведомо непригодных решений, а с другой - расширение поля поиска за счет генерирования новых подобластей. Из конкретных методологий, реализующих данное представление об эвристиках, наибольшее распространение получили так называемые лабиринтные и концептуальные эвристики.

 Скачать реферат