Мощности гармонических колебаний в электрических цепях

Проблема повышения значения “косинуса Фu” (коэффициент мощности) является одной из важнейших проблем энергетики. Это и понятно, т.к если , то необходимую полезную работу можно получить от приемника энергии при наименьшем токе в соединительных проводах, т.е. при данных значениях U и I от источника в нагрузку поступает необходимая ср

едняя мощность.

Поскольку комплексные напряжения и токи всегда удовлетворяют законам Кирхгофа, то к ним применима теорема Теледжена, согласно которой:

*

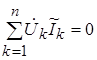, и как следствие

и .

Здесь можно ввести понятие условий баланса мощностей. Эти условия могут использоваться для проверки решений задач анализа режима ГК символическим методом.

Вывод: определение необходимых значений мощностей ГК в ЭЦ позволяет осуществить инженерный анализ результатов расчета на их правильность выполнения и оценить энергетическую эффективность всей ЭЦ или ее участка.

2. Условия передачи максимума средней мощности от генератора к нагрузке

Пусть дан источник ГК (генератор) с параметрами:

– комплексное задающее напряжение,

– внутреннее сопротивление источника.

Найдем такие значения активной R и реактивной Х составляющей составляющих комплексного сопротивления пассивной нагрузки генератора , при которой в ней выделяется максимальная средняя мощность (рисунок 1).

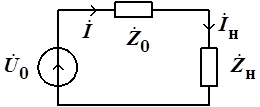
Рис. 1.

В соответствии с законом Ома ток IH в нагрузке с комплексным сопротивлением будет:

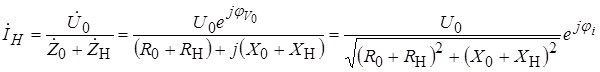где

.

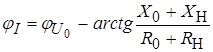При этом в нагрузке цепи выделяется средняя мощность:

.

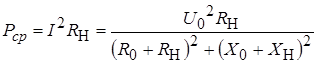Значение средней мощности изменяется в широких пределах с изменением сопротивления нагрузки. Мощность максимальна, если , т.е. при .

Это условие выполнимо, поскольку реактивная составляющая сопротивления нагрузки, т.е. двухполюсника, может принимать как положительные, так и отрицательные значения. Тогда

.

Дальнейшая задача сводится к исследованию этой зависимости как функции от переменного RH.

Очевидно, что значение функции обращается в нуль при RH = 0 и . Следовательно, при изменении RH от 0 до ¥ функция имеет по крайней мере один максимум. Используя правила исследования функции, получим условия максимума: RH = R0.

Примечание:

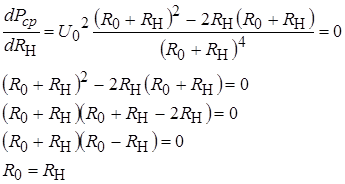
Следовательно, в режиме ГК генератор развивает максимальную мощность в нагрузке, комплексное сопротивление которой

.

Сопряжено с комплексным внутренним сопротивлением генератора

.

Нагрузку, удовлетворяющую условиям , называют сопряженной нагрузкой.

Значение максимально возможной средней мощности, которую может развить генератор на нагрузке можно показать на рисунке 2.

.

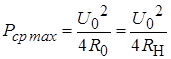Рис.2.

На рисунке сплошной линией приведен график зависимости средней мощности от соотношения . При такая же по величине мощность, как и в нагрузке, выделяется на внутреннем сопротивлении генератора . Поэтому коэффициент полезного действия (КПД) генератора, т.е. отношение отдаваемой в нагрузку и развиваемой генератором мощности, равен h = 0,5. С увеличением RH – средняя мощность уменьшается, но растет КПД. График зависимости КПД генератора показан на рисунке штриховой линией.

В энергетических системах где чрезвычайно важен высокий КПД, стремятся к тому, чтобы .

Однако, следует обратить внимание на то, что при таком режиме использование генератора значительное уменьшение RH приводит к опасному (аварийному повышению мощности, расходуемой в самом генераторе).

В целях связи часто ZH выбирают равных Z0, т.е. .

В этом случае говорят, что генератор нагружен согласованно, а сопротивление нагрузки называют согласованной.

Схема генератора, нагруженного согласованно, показана на рисунке 3. При согласованной нагрузке .

Рис. 3.

Это по сути условие обеспечения неискаженной передачи формы сигналов.

.

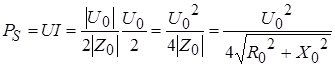При согласованной нагрузке полная, а тем более средняя мощность будет меньше или равна максимально возможной средней мощности, т.к Pcp. max получается при X0 = 0. При чисто активном сопротивлении генератора, что типично для радиотехнических устройств, понятие согласованной и сопряженной нагрузки не различаются.

Вывод: Т.О., в случае генератора с активным внутренним сопротивлением согласованное включение и максимально возможная средняя мощность в нагрузке достигается при условии равенства сопротивления нагрузки внутреннему сопротивлению генератора гармонических колебаний.

3. Особенности расчета ЭЦ с индуктивными связями

Как отмечалось ранее, применение различных методов расчета резистивных ЭЦ (МУН, МКТ, МН, МЭГ) справедливо и для режима ГК с использованием метода комплексных амплитуд (МКА). Это находит свое применение при расчетах различных схем усилителей, генераторов и т.д. Остановимся на некоторых особенностях расчета ЭЦ с индуктивными связями.

Из курса физики известно, что если две катушки имеют индуктивную связь (рисунок 4, а),

,

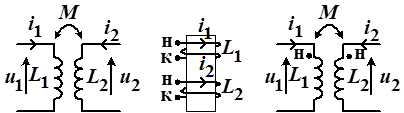а) б) в)

Рис. 4

то напряжение на зажимах одной из этих катушек представляет собой результат наложения двух составляющих: напряжения самоиндукции и напряжения взаимоиндукции, т.е.

 Скачать реферат