К механизму электропроводности магнитной жидкости с графитовым наполнителем

, (3)

где – обратный гиперболический тангенс: 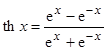. Из (3) следует, что

, (4)

то есть для проводящей сферы формула (2) принимает ви

д

, (5)

где - радиус сферы. Если же сфера является диэлектриком, то в этом случае формула (5) имеет вид [5]

, (6)

где – относительная диэлектрическая проницаемость сферы. При из (6) получается выражение (5) для проводящей сферы. Поэтому предлагаемый ниже механизм электропроводности можно применить и для случая с диэлектрическим наполнителем эллипсоидальной формы.

Накапливающиеся на проводящем эллипсоиде заряды порождают отталкивающее поле, препятствующее приходу новых заряженных частиц магнетита. Отталкивающее поле вблизи эллипсоида задается формулой [5]

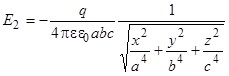, (7)

где – заряд, накапливающийся на поверхности эллипсоида; – число заряженных частиц магнетита, несущих элементарный заряд . Для случая сферы формула (7) принимает вид

. (8)

В результате суперпозиции получим результирующее поле, направленное перпендикулярно поверхности эллипсоида. Результирующее поле равно

. (9)

Причем при

. (10)

Так как в формуле (2) выражение под корнем есть медленно меняющаяся функция, то можно ее приблизительно заменить средним значением:

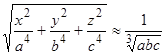. (11)

Тогда выражения для и можно приближенно записать в виде

, (12)

. (13)

Тогда для результирующего поля запишем

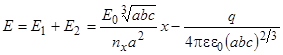. (14)

Для нахождения потока вектора напряженности электрического поля по формуле (1), нам необходимо знать выражение для элемента площади поверхности эллипсоида вращения, которое согласно [6] имеет вид

. (15)

С учетом (14) и (15) выражение (1) для потока вектора напряженности получим

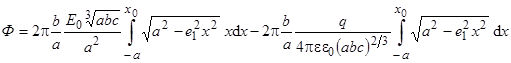. (16)

Интегралы в формуле (16) элементарно интегрируются [7]:

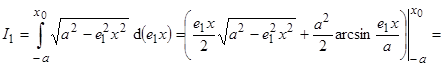
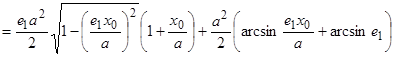. (17)

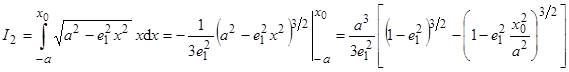.(18)

С учетом формул (17) и (18) выражение для потока вектора напряженности примет вид

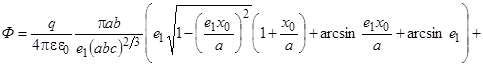
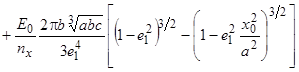. (19)

Упростим выражение (19), принимая во внимание, что .

. (20)

Насыщение частицы графита зарядом произойдет, когда поток вектора напряженности станет равным нулю. То есть заряжение частиц графита будет происходить до тех пор, пока индуцированный заряд не будет скомпенсирован. Из условия найдем предельный заряд частицы графита для случая, когда магнитное поле параллельно электрическому полю:

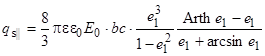. (22)

Предельное число заряженных частиц магнетита с элементарным зарядом e, отдающих заряд частице графита, в электрическом поле с напряженностью равно: .

2. Магнитное поле перпендикулярно электрическому полю. Рассмотрим, что произойдет, если частица графита под действием магнитного поля будет ориентирована перпендикулярно электрическому полю. Как было отмечено выше, если частица графита представляет собой сферу, то никаких изменений не произойдет. Если частица графита представляет собой вытянутый эллипсоид, то она большей полуосью, а значит, большей площадью поперечного сечения, будет расположена перпендикулярно току.

Пусть в результате такой ориентации полуось эллипсоида параллельна оси . В этом случае напряженность электрического поля Е1 вблизи поверхности проводящего эллипсоида определяется выражением (2), в котором необходимо заменить на

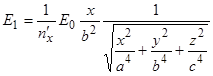, (23)

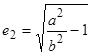, . (24)

Отталкивающее поле вблизи эллипсоида задастся формулой (7)

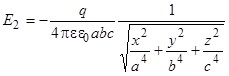. (25)

Результирующее поле запишется в виде

. (26)

Из условия находим :

. (27)

Аналогично, запишем приближенные выражения для и в виде

, (28)

. (29)

Для результирующего поля запишем

 Скачать реферат