К механизму электропроводности магнитной жидкости с графитовым наполнителем

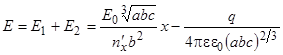. (30)

Выражение для элемента площади поверхности эллипсоида вращения в этом случае имеет вид

. (31)

Поток вектора напряженности электрического поля в этом случае определится формулой

.

(32)

Из условия найдем предельный заряд частицы графита для случая, когда магнитное поле перпендикулярно электрическому полю:

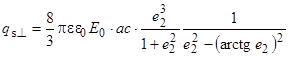. (33)

Введем следующие обозначения

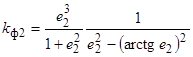, , (34)

которые назовем коэффициентами формы, соответственно, для эллипсоида, расположенного параллельно току, и перпендикулярно току. Тогда выражения для предельных зарядов, соответственно, запишутся в виде

, (35)

. (36)

Расчеты по формулам (35) и (36) показывают, что . Таким образом, частица графита ориентированная перпендикулярно электрическому полю заряжается больше, чем в случае, когда она ориентирована параллельно электрическому полю. Это приводит к уменьшению основного тока.

3. Удельная проводимость магнитной жидкости с графитовым наполнителем. Если бы описанный выше механизм не имел бы место, то невозмущенный ток можно записать, согласно определению [4], в виде

, (37)

где – плотность невозмущенного тока; – площадь обкладок ячейки [1]. Плотность тока записывается в виде [4]

, (38)

где – концентрация заряженных частиц магнетита в невозмущенном потоке; – удельная проводимость магнитной жидкости при отсутствии частиц графита; – скорость упорядоченного движения заряженных частиц магнетита. Отсюда удельную проводимость записывают в виде [4]

, , (39)

где – подвижность заряженных частиц магнетита; – объемный заряд невозмущенного потока.

Концентрацию частиц графита обозначим . В выражении для плотности тока необходимо учесть, что часть объемного заряда оседает на частицах графита и не участвует в токе. Поэтому для плотности тока, когда магнитное поле направлено параллельно электрическому полю, можно записать

. (40)

Отсюда для удельной проводимости получим

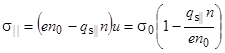. (41)

Аналогично, получим выражение для удельной проводимости, когда магнитное поле направлено перпендикулярно току:

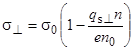. (42)

Из (41) и (42) следует

. (43)

Учитывая, что , то (43) можно приближенно записать в виде

. (44)

Из (44) видно, что когда магнитное поле параллельно току, то удельная проводимость больше, чем когда магнитное поле перпендикулярно току. Аналогично, из (41) и (42) запишем выражения для удельных сопротивлений

, , (45)

где и – удельные сопротивления магнитной жидкости с графитовым наполнителем в магнитном поле, соответственно, параллельном электрическому полю и перпендикулярному электрическому полю; – удельное сопротивление магнитной жидкости в отсутствии частиц графита. В эксперименте [1] измерялось сопротивление ячейки. Соответственно, для сопротивлений запишем выражения

, , (46)

где – сопротивление магнитной жидкости в отсутствии частиц графита. Отсюда

, (47)

где . Откуда видно, что сопротивление ячейки в магнитном поле, параллельном электрическому полю, меньше, чем в магнитном поле, перпендикулярном электрическому полю.

Сделанный вывод согласуются с данными экспериментальных исследований, результаты которых приведены на рисунке.

Таким образом, из вышеизложенного следует, что проводимость магнитной жидкости с графитовым наполнителем изменяется в зависимости от направления магнитного поля. Проводимость магнитной жидкости с графитовым наполнителем в магнитном поле, параллельном электрическому полю больше, чем в магнитном поле, перпендикулярном электрическому полю: .

4. Расчеты. Из формулы (47) следует, что анизотропия электрических свойств магнитной жидкости с графитовым наполнителем будет существенно зависеть от концентрации частиц графита, что действительно наблюдалось в эксперименте [1]. При малых концентрациях частиц графита эффект не существенен.

Концентрацию частиц графита найдем по формуле [8]

, (48)

где – объемная концентрация частиц графита. В эксперименте [1] объемная концентрация была равна , а радиус частиц графита был порядка мкм. Подставляя численные значения в (48), для полной концентрации частиц графита получим м-3. Примем мкм, мкм. Это соответствует эксцентриситетам и , соответственно, коэффициенты формы и . Примем . Объемный заряд, оседающий на частицах графита, равен Кл/м3. На частицу графита, расположенную перпендикулярно току, оседает на заряженных частиц магнетита больше, чем на частицу, расположенную параллельно току.

 Скачать реферат