Исследование нелинейных цепей постоянного тока

Отсюда следует, что, строго говоря, дифференциальное сопротивление характеризует нелинейный элемент в точке ВАХ, для которой оно определяется.

Тем не менее, поскольку для рассматриваемого случая (рис. 8) колебания напряжения ( или ) невелики, с достаточной для практики точностью можно считать, что каждая точка участка ВАХ от до характеризуется постоянной величиной :

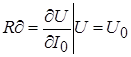
Дифференциальное сопротивление можно определить и графически, как тангенс угла между касательной в рабочей точке ВАХ и осью токов (рис. 8) в направлении от оси токов до касательной по часовой стрелке:

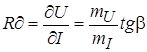
Вернёмся к рассматриваемому случаю. Поскольку ВАХ на участке заменяется прямой линией, то напряжение можно представить в виде суммы двух слагаемых (рис. 8):

(1)

Учитывая, что со временем положение рабочей точки изменяется в пределах к соотношению (1) необходимо добавить слагаемое , которое определяет некоторый источник ЭДС переменного тока с амплитудным значением или :

(2)

Соотношение (2) определяет схему замещения нелинейного резистивного элемента (рис. 9), в которой он заменяется линейным резистивным элементом с сопротивлением и двумя источниками ЭДС.

Рассмотренные приёмы называются линеаризацией ВАХ нелинейного элемента. Эти приёмы позволяют, при указанных условиях, свести нелинейную цепь к линейной. В случае широкого диапазона изменения рабочей точки ВАХ или повышенных требований к точности расчёта используют аналитические или графические методы.

Рассмотрим метод преобразований и расчёта цепей с нелинейными элементами, основанный на предварительной замене электрической цепи цепью, имеющей эквивалентную ВАХ и последующего перехода в процессе расчёта к заданной электрической цепи. Этот метод является графическим методом расчёта.

Положим, что нелинейные элементы соединены последовательно (рис. 10) и имеют известные ВАХ (рис. 11). Если задан ток в такой цепи (например, на рис. 11), то, т.к. при последовательном соединении элементов ток в каждом элементе будет одинаковым и равным , падение напряжения на каждом элементе ( и ) находится непосредственно по ВАХ этого элемента без каких – либо дополнительных построений (рис. 11).

Если же задано общее напряжение , то без дополнительных построений определить в таком соединении элементов (рис. 10) ток и падения напряжения достаточно сложно. Для этого необходимо построить эквивалентную ВАХ:

Построение эквивалентной ВАХ основано на следующих особенностях последовательного соединения элементов (рис. 10):

- ток в такой цепи, протекающий через каждый элемент один и тот же;

- общее напряжение, приложенное ко всей цепи, равно сумме падений напряжений и на каждом элементе:

Из сказанного следует, что при любом произвольно взятом токе, соответствующая точка эквивалентной ВАХ находится суммированием абсцисс точек исходных ВАХ и , определённых при том же токе.

Данное правило позволяет следующим образом построить эквивалентную ВАХ (рис. 12). Задаются несколькими произвольно взятыми значениями тока в цепи ( по оси ординат на рис.12); по исходным ВАХ , находят соответствующие каждому току напряжения и . Суммированием и определяют абсциссы точек эквивалентной ВАХ. Их ординаты заданы произвольно выбранными точками . Соединяя плавной линией полученные точки , получают график эквивалентной ВАХ .

Теперь зная, например, что , по эквивалентной ВАХ определяют ток , а затем по исходным ВАХ и находят падение напряжения на каждом элементе , . Т.о. производится графический расчёт параметров режима работы цепи из последовательно соединённых нелинейных резистивных элементов.

В случае если один из последовательно соединённых резистивных элементов является линейным (рис. 13), графический расчёт производят методом нагрузочной характеристики.

Пусть дана схема (рис. 13), в которой , . Для неё согласно 2-го закона Кирхгофа можно записать:

 Скачать реферат