Изучение вращательного движения на приборе Обербека. Упругие и неупругие удары шаров

Коэффициент восстановления скорости можно найти по следующей формуле:

9) .

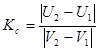Если при соударении потеря кинетической энергии отсутствует (Kс = 1), то удар называется абсолютно упругим, а при Kс = 0 абсолютно неупругим. Если же 0 < Kс < 1, то удар является не вполне упругим.

Применительно к соударяющимся шарам, один

из которых покоится, формулу (4) можно записать так:

10) ,

а для абсолютно неупругого удара .

Скорости шаров до и после удара можно определить по формулам:

11) ; 12) ; 13)

где l – расстояние от точки подвеса до центра тяжести шаров (l = 470 ± 10 мм.), a0 – угол бросания правого шара, a1 и a2 – углы отскока соответствующих шаров.

Расчет вращательного движения на приборе Обербека

После снятия показаний с установки имеем значения следующих величин:

mпл = 58,8×10-3 кг. (масса платформы);

m1 = 55,7×10-3 кг. m2 = 56,5×10-3 кг. m3 = 55,8×10-3 кг. (массы 3-х дополнительных грузов закреплённых на платформе);

4m = 745×10-3 кг. (масса 4-х одинаковых грузов закреплённых на крестовине установки);

I0 = 2,37×10-2 кг×м2. (момент инерции ненагруженной крестовины);

l = 27×10-2 м. (длина стержней крестовины);

h = 0,4 м. (путь пройденный грузом);

При дальнейших расчётах следует учесть, что масса груза (m0) складывается из массы платформы (mпл) и массы всех дополнительных грузов установленных на платформе:

m0 = mпл + m1 + m2 + m3; m0 = 226,8×10-3 кг.

Рассматривая все случаи снятия измерений, по формуле (10) подсчитаем отношение M/e (момент инерции маховика) для каждого из них.

Измерения при R1 и d1: Измерения при R1 и d2:

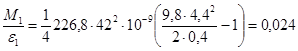кг×м2.

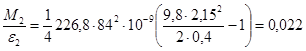кг×м2.

Измерения при R2 и d1: Измерения при R2 и d2:

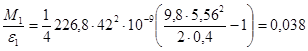кг×м2.

кг×м2.

Измерения при R3 и d1: Измерения при R3 и d2:

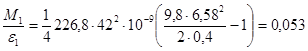кг×м2.

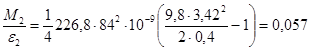кг×м2.

По формуле (12) определим величину момента инерции маховика Обербека.

Теперь определим величину момента инерции данного маховика по формуле (12). По данной формуле искомая величина вычисляется только через I0, 4m и R, а следовательно не зависит от di (диаметра шкива, жестко связанного с маховиком). Определяя величину момента инерции данной системы тел рассматриваем только 3 случая измерений, каждый случай для своего Ri

Измерения при R1:

I = 2,37×10-2 + 745×10-3×0,12 = 0,031 кг×м2.

Измерения при R2:

I = 2,37×10-2 + 745×10-3×0,152 = 0,04 кг×м2.

Измерения при R3 и d1:

 Скачать реферат