Физические основы современных представлений в теории электромагнитного поля
![]() .
.
Эти рассуждения описывают результат электрической поляризации, а электростатической теоремой Гаусса их называют по той причине, что она тождественно устанавливает: ![]() . Правда, обычно в физические подробности процесса поляризации не вникают, а потому о поляризаци
. Правда, обычно в физические подробности процесса поляризации не вникают, а потому о поляризаци
онном заряде ![]() просто не говорят. Здесь первые два интеграла это определение вектора
просто не говорят. Здесь первые два интеграла это определение вектора ![]() - численно равного поверхностной плотности поляризационного заряда
- численно равного поверхностной плотности поляризационного заряда ![]() на пробной площадке, ориентация которой такова, что
на пробной площадке, ориентация которой такова, что ![]() на ней максимальна, при этом нормаль
на ней максимальна, при этом нормаль ![]() к поверхности площадки коллинеарна вектору
к поверхности площадки коллинеарна вектору ![]() . В системе электродинамических дифференциальных уравнений (1) теорема Гаусса представлена (см. теорему Гаусса-Остроградского) соотношением (1б), описывающим результат электрической поляризации материальной среды, где в случае ее электронейтральности (
. В системе электродинамических дифференциальных уравнений (1) теорема Гаусса представлена (см. теорему Гаусса-Остроградского) соотношением (1б), описывающим результат электрической поляризации материальной среды, где в случае ее электронейтральности (![]() ) оно имеет вид
) оно имеет вид ![]() .
.
Воспользуемся теперь другим первичным фундаментальным законом электромагнетизма - законом сохранения электрического заряда (5), структурно представляющим собой уравнение непрерывности. Закон гласит: изменение во времени заряда ![]() в данной точке пространства единственно возможно лишь за счет транспорта зарядов извне
в данной точке пространства единственно возможно лишь за счет транспорта зарядов извне ![]() , ведь по определению (теорема Гаусса-Остроградского) дивергенция - это объемная плотность потока векторного поля в данной точке. Тогда подстановка в (5) уравнения (1б) дает формулу
, ведь по определению (теорема Гаусса-Остроградского) дивергенция - это объемная плотность потока векторного поля в данной точке. Тогда подстановка в (5) уравнения (1б) дает формулу ![]() . И с учетом того, что для любого векторного поля
. И с учетом того, что для любого векторного поля ![]() , получаем еще одно уравнение обсуждаемой системы:
, получаем еще одно уравнение обсуждаемой системы: ![]() (1в). Это уравнение называют законом полного тока: электрические токи проводимости и смещения порождают вихревое магнитное поле, силовые линии векторов напряженности
(1в). Это уравнение называют законом полного тока: электрические токи проводимости и смещения порождают вихревое магнитное поле, силовые линии векторов напряженности ![]() которого охватывают линии этих токов.
которого охватывают линии этих токов.
Итак, в области существования движущихся зарядов и переменных во времени электрических полей ![]() , то есть в уравнении (1в) функция
, то есть в уравнении (1в) функция ![]() является вихревой, а потому для математического уточнения данной топологии магнитного поля введем соотношение калибровки
является вихревой, а потому для математического уточнения данной топологии магнитного поля введем соотношение калибровки ![]() . Тем самым получим следующее уравнение системы (1) – уравнение (1г). Поскольку дивергенция - объемная плотность потока векторного поля в данной точке, то уравнение
. Тем самым получим следующее уравнение системы (1) – уравнение (1г). Поскольку дивергенция - объемная плотность потока векторного поля в данной точке, то уравнение ![]() способно описать не только вихревые свойства функции
способно описать не только вихревые свойства функции ![]() , но и ее потенциальную версию, случай когда
, но и ее потенциальную версию, случай когда ![]() . Таким образом, соотношение (1г) математически представляет физический результат магнитной поляризации материальной среды.
. Таким образом, соотношение (1г) математически представляет физический результат магнитной поляризации материальной среды.
Наконец, частным дифференцированием по времени ![]() уравнения (1г) получаем на основе
уравнения (1г) получаем на основе ![]() адекватное с учетом знака закону электромагнитной индукции Фарадея уравнение (1а), последнее в системе (1). Итак, изменяющееся во времени поле магнитной индукции порождает в данной точке пространства вихревое электрическое поле. Ввиду того, что в уравнении (1a)
адекватное с учетом знака закону электромагнитной индукции Фарадея уравнение (1а), последнее в системе (1). Итак, изменяющееся во времени поле магнитной индукции порождает в данной точке пространства вихревое электрическое поле. Ввиду того, что в уравнении (1a) ![]() , то функция поля
, то функция поля ![]() является вихревой, и эту топологию способно уточнить, согласно вышесказанному о дивергенции, уже полученное нами ранее уравнение (1б) в виде
является вихревой, и эту топологию способно уточнить, согласно вышесказанному о дивергенции, уже полученное нами ранее уравнение (1б) в виде ![]() . Как видим, дивергентные уравнения (1б) и (1г) как математически, так и физически весьма содержательны. И это только то, что лежит на поверхности.
. Как видим, дивергентные уравнения (1б) и (1г) как математически, так и физически весьма содержательны. И это только то, что лежит на поверхности.
Кстати, с методической точки зрения поучительно указать, что подобный подход, а именно использование фундаментальных базовых соотношений физики, позволяет получить и основное уравнение корпускулярно-волнового дуализма квантовой механики – так называемое уравнение Шрёдингера. Известно [2], что представления указанного дуализма основаны на введенной Планком энергии фотона ![]() и длины волны де-Бройля
и длины волны де-Бройля ![]() движущейся микрочастицы:
движущейся микрочастицы:
а) ![]() , б)
, б) ![]() , (6)
, (6)
где ![]() - модифицированная постоянная Планка,
- модифицированная постоянная Планка, ![]() - частота фотона,
- частота фотона, ![]() - механический импульс частицы.
- механический импульс частицы.
Расширяя понятие энергии ![]() фотона как некой частицы на произвольную материальную микрочастицу, попытаемся сопоставить выражения для плоской скалярной монохроматической волны в комплексной экспоненциальной форме с законом сохранения механической энергии:
фотона как некой частицы на произвольную материальную микрочастицу, попытаемся сопоставить выражения для плоской скалярной монохроматической волны в комплексной экспоненциальной форме с законом сохранения механической энергии:
а) ![]() , б)
, б) ![]() . (7)
. (7)
Сопоставляя (7а) с (6), имеем: ![]() и
и ![]() . И в итоге получаем выражение волновой функции
. И в итоге получаем выражение волновой функции 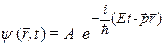 , содержащей в себе основные представления корпускулярно-волнового дуализма Материи.
, содержащей в себе основные представления корпускулярно-волнового дуализма Материи.
А теперь подставим полученную волновую функцию в закон сохранения энергии (7б), и цепочкой логически последовательных рассуждений:
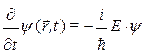
![]()
 ;
;

![]()
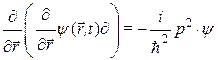
![]()
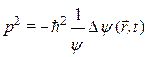
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода
