Физические основы современных представлений в теории электромагнитного поля
Говоря более конкретно, фундаментальность корпускулярно-полевого дуализма Материи обусловлена тем, что как две стороны одной медали локальные характеристики микрочастицы (совокупно, и макрообъекта) находятся в неразрывной связи с ее собственными полевыми параметрами. Электрическому заряду ![]() , кратному кванту электрического потока - з
, кратному кванту электрического потока - з
аряду электрона |e-|, соответствует электрический векторный потенциал ![]() , а удельному (на единицу заряда) моменту, кратному кванту магнитного потока
, а удельному (на единицу заряда) моменту, кратному кванту магнитного потока ![]() , отвечает магнитный векторный потенциал
, отвечает магнитный векторный потенциал ![]() , при этом ориентации векторов полей
, при этом ориентации векторов полей ![]() и
и ![]() взаимно ортогональны. В итоге приходим к выводу, что электромагнитные вектор-потенциалы – это истинные поля частиц микромира, а не их весьма спорная, почти мифическая волновая функция плотности вероятности
взаимно ортогональны. В итоге приходим к выводу, что электромагнитные вектор-потенциалы – это истинные поля частиц микромира, а не их весьма спорная, почти мифическая волновая функция плотности вероятности ![]() .
.
Знаменательно здесь то, что указанные электромагнитные векторные потенциалы - собственные поля частиц Материи, являющиеся полевыми эквивалентами их корпускулярных (локальных) характеристик непосредственно следуют из уравнений классической электродинамики (1), первоначальная версия которых появилась еще во второй половине 19 века обобщением Дж.К. Максвеллом [9] эмпирических фактов того времени в этой области знания.
Итак, мы видим, что векторные потенциалы – это полноправные физически значимые поля, и учет этого обстоятельства должно нам позволить углубить и кардинально модернизировать концептуальные основы классической электродинамики, где, в частности, необходимо ожидать, что обсуждаемая здесь система уравнений Максвелла будет лишь рядовым частным следствием.
Покажем конкретно, какую же роль играют векторные потенциалы в электромагнитных процессах и явлениях? Очевидно, здесь четко прослеживается реальная возможность обратить проведенные выше рассуждения вспять, поскольку из обсуждаемой концепции «корпускулярно-полевого дуализма» физических характеристик микрочастицы необходимо следуют электродинамические уравнения современной теории электромагнитного поля на базе системы соотношений первичной взаимосвязи ЭМ поля с компонентами электрической ![]() и магнитной
и магнитной ![]() напряженности и ЭМ векторного потенциала с электрической
напряженности и ЭМ векторного потенциала с электрической ![]() и магнитной
и магнитной ![]() компонентами:
компонентами:
(а) ![]() , (б)
, (б) ![]() ,
,
(в) ![]() , (г)
, (г) ![]() , (15)
, (15)
(д) ![]() , (е)
, (е) 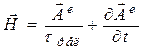 .
.
Объединение соотношений (9) – (12) в систему взаимосвязанных уравнений (15) представляется весьма конструктивным, поскольку в этом случае возникает система дифференциальных уравнений, описывающих значительно более сложное и необычное с точки зрения общепринятых воззрений вихревое векторное поле, состоящее из совокупности функционально связанных между собой четырех вихревогполевых компонент. Конкретно оно состоит из реально наблюдаемых в эксперименте полей векторов электрической ![]() и магнитной
и магнитной ![]() напряженностей - поля электромагнитного силового взаимодействия частиц Материи и ненаблюдаемых напрямую полей электрического
напряженностей - поля электромагнитного силового взаимодействия частиц Материи и ненаблюдаемых напрямую полей электрического ![]() имагнитного
имагнитного ![]() векторных потенциалов - собственного электромагнитного поля частиц Материи, полевого эквивалента их локальных характеристик: заряда и спина, которые также напрямую ненаблюдаемы, а лишь опосредовано изучением их полей взаимодействия. Такое четырехкомпонентное векторное поле физически логично назвать реальным электромагнитным полем.
векторных потенциалов - собственного электромагнитного поля частиц Материи, полевого эквивалента их локальных характеристик: заряда и спина, которые также напрямую ненаблюдаемы, а лишь опосредовано изучением их полей взаимодействия. Такое четырехкомпонентное векторное поле физически логично назвать реальным электромагнитным полем.
Объективность существования указанного четырехкомпонентного вихревого поляиллюстрируется нетривиальными следствиями из полученных выше соотношений, поскольку подстановки (15д) в (15в) и (15е) в (15a) приводят к системе новых электродинамических уравнений, структурно аналогичной системе традиционных уравнений Максвелла (1), но уже для поля ЭМ векторного потенциала с электрической ![]() и магнитной
и магнитной ![]() компонентами:
компонентами:
(a) ![]() , (б)
, (б) ![]() , (16)
, (16)
(в)  , (г)
, (г) ![]() .
.
Чисто вихревой характер компонент поля векторного потенциала обеспечивается условием калибровки - дивергентными уравнениями (16б) и (16г).
Соответственно, аналогичные математические операции с соотношениями (15) позволяют получить еще две других системы уравнений [7]:
для электрического поля с компонентами ![]() и
и ![]()
(a)  , (б)
, (б) ![]() , (17)
, (17)
(в) ![]() , (г)
, (г) ![]()
и для магнитного поля с компонентами ![]() и
и ![]() :
:
(a) 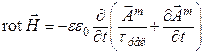 , (б)
, (б) ![]() , (18)
, (18)
(в) ![]() , (г)
, (г) ![]() .
.
Таким образом, уравнения системы (15) первичной взаимосвязи компонент ЭМ поля и поля ЭМ векторного потенциала, безусловно, фундаментальны. Кстати, если считать соотношения (15) исходными, то из них подобным образом [8] следуют и уравнения системы (1), справедливые для локально электронейтральных сред (![]() ). Существенно здесь и также то, что в системах (1), (16) - (18) их дивергентные уравнения представляют собой начальные условия в математической задаче Коши для соответствующих роторных уравнений, что делает эти системы уравнений замкнутыми.
). Существенно здесь и также то, что в системах (1), (16) - (18) их дивергентные уравнения представляют собой начальные условия в математической задаче Коши для соответствующих роторных уравнений, что делает эти системы уравнений замкнутыми.
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода
