Физические основы современных представлений в теории электромагнитного поля

построить предварительное дифференциальное соотношение

.

В итоге, окончательно получаем основное уравнение квантовой механики пространственно-временное (волновое) уравнение Шрёдингера [2]:

, (8)

физически представляющее собой запись закона сохранения механической энергии микрочастицы, записанного в волновой форме.

Далее можно получить стационарное уравнение Шрёдингера, используя подстановку в (8) волновой функции в виде :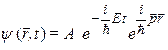

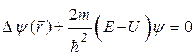. (8*)

Итак, как и должно быть, в настоящей физике все относительно просто и понятийно ясно, надо только размышлять над получаемой информацией и анализировать ее. Как говорили в Китае за II тысячелетия до нашей эры: «Знания без размышлений бесполезны, а размышления без знаний опасны!».

А мы опять возвратимся к обсуждению уравнений Максвелла, где следует отметить весьма ограниченный диапазон явных возможностей уравнений Максвелла при описании ряда известных в настоящее время явлений электромагнетизма. В частности, уравнения (1) не могут вскрыть и адекватно описать физическую суть магнитных явлений, поскольку истинный магнетизм – это спиновый магнетизм [2]. Например, они в принципе не способны объяснить эффект Эйнштейна-де Гааза [1, 2], когда в материальной среде при ее однородном намагничивании возникает механический момент вращения, направленный коллинеарно подмагничивающему полю магнитной индукции . Так же далеко не ясен вопрос о существовании и физической реализации момента импульса электромагнитного поля, соответственно, переносящих его волн.

Здесь как бы существует парадокс, где с одной стороны, теория Максвелла предсказывает равенство нулю момента импульса плоской электромагнитной волны, а, с другой, физически понятно, что электромагнитное излучение – это излучение возбужденными атомами избытка энергии в виде фотонов, которые будут забирать от атома не только часть энергии, но и уносить долю внутреннего углового момента атома. Следовательно, распространяющееся в виде волн электромагнитное поле должно обладать вполне определенной величиной момента импульса, что, кстати, наблюдалось в экспериментах [4, 5].

Таким образом, главный и принципиальный дефект традиционной классической электродинамики в том, что в ее представлениях об электрическом заряде и его поле нет понятия о спине (собственном моменте импульса). Ссылки на ныне существующую квантовую электродинамику [2] неуместны, поскольку это отдельная самостоятельная наука, по сути несвязанная с классической теорией. Правда, известны попытки введения в электродинамику так называемого классического спина [6], но и они оказались неконструктивными.

Попытаемся исправить сложившуюся ситуацию, поскольку если взглянуть глубже, то те же дивергентные уравнения (1б) и (1г) содержат сведения о полях электрического и магнитного векторных потенциалов, физический смысл которых, несмотря на определенный прогресс в установлении их физической значимости [7, 8], и по сей день концептуально не понят, а потому в теории электромагнетизма эти не наблюдаемые напрямую поля остаются в должной мере не принятыми и, в сущности, не используемыми. Итак, разберемся в этом вопросе, для чего воспользуемся обсуждаемой здесь системой уравнений (1).

Представления о векторных потенциалах определяются очевидным положением о том, что дивергенция ротора любого векторного поля тождественно равна нулю: . Поэтому магнитную компоненту векторного потенциала можно ввести посредством соотношения системы уравнений (1), описывающим магнитную поляризацию (намагниченность) материальной среды, а электрическую компоненту - соотношением , описывающим поляризацию локально электронейтральной () среды:

(а) , (б) . (9)

Таким образом, с точки зрения физического смысла векторные электромагнитные потенциалы непосредственно связаны с электрической и магнитной поляризациями, а потому их можно называть поляризационными потенциалами.

Тогда подстановка соотношения для магнитного векторного потенциала (9a) в уравнение вихря электрической напряженности (1а) приводит к известной формуле связи поля вектора указанной напряженности с магнитным векторным потенциалом [1]:

, (10)

описывающей закон электромагнитной индукции Фарадея. Здесь электрический скалярный потенциал: принципиально не рассматривается, как не имеющий отношения к обсуждаемым в работе вихревым полям.

При аналогичной подстановке соотношения для электрического векторного потенциала (9б) в уравнение вихря магнитной напряженности (1в) с учетом закона Ома получаем в итоге связь этой напряженности с указанным векторным потенциалом:

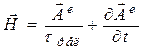. (11)

Здесь - постоянная времени релаксации электрического заряда в среде за счет ее электропроводности.

Однозначность функций векторных потенциалов, то есть чисто вихревой характер таких полей обеспечивается условием кулоновской калибровки:

(а) , (б) , (12)

где абсолютные электрическая и магнитная проницаемости, согласно соотношениям (10) и (11), соответствуют в формулах (12) конкретным компонентам векторного потенциала.

Как видим, векторные потенциалы принципиально сопровождают явления электрической и магнитной поляризаций материальной среды, причем, согласно (9), пары векторов и , и - взаимно ортогональны; соответственно, согласно (10) и (11), другие векторные пары и , и - взаимно коллиненарны. Покажем, что векторные потенциалы – это не математические фикции, а физически значимые фундаментальные поля, порождающие (см. соотношения (10) и (11)) традиционные вихревые электромагнитные поля.

 Скачать реферат