Анализ стационарных и динамических объектов в MathCAD

2. Анализ нелинейных стационарных объектов

Цель работы: исследовать параметры нелинейных стационарных объектов, описываемых системами нелинейных алгебраических уравнений, используя для их решения средства пакета MathCAD.

Содержание работы:

1) изучить теоретические положения (раздел 2.1), раскрывающие структуру нелинейных стационарных объектов, и

х математическое описание и пример решения систем нелинейных алгебраических уравнений средствами пакета MathCAD, используемый для анализа такого рода объектов;

2) выполнить индивидуальное задание согласно предусмотренной в разд.2.2 последовательности выполнения работы;

3) оформить описание раздела по контрольной работе согласно требованиям задания.

2.1. Краткие теоретические сведения

Структура и математическая модель объекта

Структурная схема нелинейного стационарного объекта имеет вид:

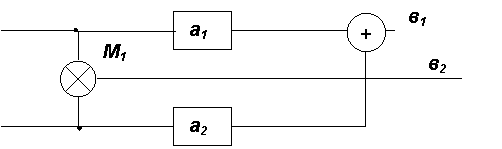
Такой объект представляет собой систему, которая имеет два входа х1 и х2 с постоянными значениями в установившемся режиме и два выхода в1 и в2. Структура объекта определяется сумматором S1 , умножителем М1, двумя линейно– усилительными блоками а1 , а2 и системой связей между ними.

В отличие от линейных стационарных объектов нелинейные описываются системами нелинейных алгебраических уравнений.

Математическая модель, соответствующая такой схеме, имеет вид:

а1х1 +а2х2=в1;

х1х2=в2

2.1.2. Анализ объектов

Исследование такого рода объектов состоит в определении значений входных воздействий х1 ,х2 в зависимости от значений выходов в1 и в2 при заданных параметрах объекта а1 и а2 .

Реализация решения задачи исследования нелинейного стационарного объекта в такой постановке может быть осуществлена с помощью средств системы символьной математики MathCAD 7.0 PRO .

2.1.3. Решение нелинейных алгебраических и трансцендентных уравнений

2.1.3.1. Постановка задачи.Пусть дано уравнение

, (2.1)

где функция определена и непрерывна на некотором интервале (А,В). Всякое значение , обращающее функцию в нуль, то есть такое, при котором , называется корнем уравнения (2.1), а процесс нахождения называется его решением.

Если функция представляет собой многочлен относительно , то уравнение называется нелинейным алгебраическим (например, ); если в функцию входят элементарные (тригонометрические, логарифмические, показательные и т.п.) функции, то такое уравнение называется трансцендентным (например, ).

2.1.3.2. Характеристика методов. Методы решения нелинейных алгебраических и трансцендентных уравнений (НАТУ) делятся на прямые и итерационные. Первые позволяют найти решение непосредственно с помощью формул и всегда обеспечивают получение точного решения. Однако прямые методы имеются только для ограниченного круга уравнений, поэтому на практике более широко используются итерационные методы.

В итерационных методах процедура решения задается в виде многократного применения некоторого алгоритма. Полученное решение всегда является приближенным, хотя может быть сколь угодно близким к точному.

В общем случае задача решается в 2 этапа:

определение приближенных значений корней уравнения;

уточнение корней до заданной степени точности с помощью одного из итерационных методов.

Для определения приближенных значений корней уравнения используются:

1) Построение графика функций и приближенное определение точек, где кривая пересекает ось Х.

Запись уравнения в виде и построение графиков двух функций: и . Точка их пересечения и есть корень исходного уравнения (5.1).

На втором этапе происходит уточнение корня с использованием критерия окончания итерационного процесса.

Итерационный процесс следует оканчивать, когда < , т.е. при близости двух последовательных приближений к корню.

Одним из итерационных методов для уточнения корня является метод Ньютона.

2.1.3.3. Метод Ньютона

2.1.3.3.1. Геометрическая интерпретация метода Ньютона. Геометрическая интерпретация метода Ньютона показана на рис 2.1.

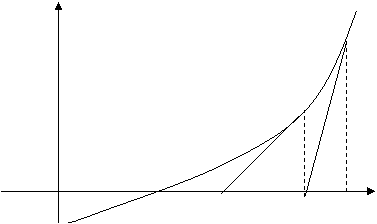
Рис. 2.1. Метод Ньютона

Приняв в качестве начального приближения к корню некоторое значение , восстанавливаем перпендикуляр в точке к оси Х. В точке пересечения перпендикуляра с графиком функции , для которой отыскивается нуль, проводим касательную к кривой. Точка пересечения касательной с осью Х дает новое приближение к корню. После этого процесс повторяем для точки , получаем точку и т.д.

 Скачать реферат