Анализ стационарных и динамических объектов в MathCAD

Для формирования матрицы Якоби получим частные производные:

Подставив в (2.5) в качестве: матрицы коэффициентов (А) – частные производные функций и вектора свободных членов (В) – функции с противоположным знаком, получим запись СЛАУ в виде:

(2.7)

Задав

шись некоторым начальным приближением () и, подставив его вместо () в систему (2.7), решим полученную систему линейных уравнений (например, матричным способом ) и получим значение поправок . Если поправки не будут достаточно малы (т.е. условие < не выполняется), то вычисляется очередное приближение к корням: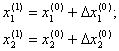

С полученным затем повторяют те же операции, что и с для получения и, если необходимо, и т.д. до тех пор, пока все получаемые поправки не будут достаточно малы, что свидетельствует о близости приближенного решения к истинному.

2.2. Последовательность выполнения работы

Согласно номеру по списку группы выбрать из табл.2.1 значения параметров для нелинейного объекта. По формулам

в1і= в1–h(і-1) ;

в2і= в2–h(і-1) ;

для і=1,2, .5 определить значения коэффициентов, определяющих выход для пяти рассматриваемых случаев.

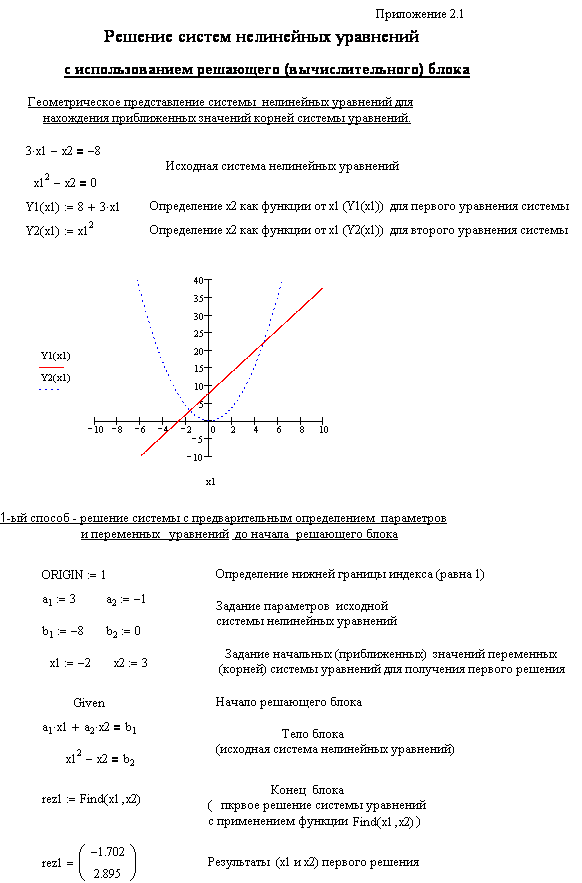
2. Составить и отладить программу решения системы нелинейных уравнений согласно Приложению 2.1 и для полученных в пункте 1 значений выхода найти пять наборов значений входных переменных х1 и х2 .

3. По результатам просчета на ПЭВМ получить таблицы значений входа (х1 и х2 ) при заданных значениях выхода ( в1 и в2).

4. Построить графики изменения значений х1 и х2 в зависимости от значений в1 и в2. .

Таблица 2.1

3. Анализ динамических объектов

Цель работы: исследовать свойства и поведение динамических объектов, описываемых системами обыкновенных нелинейных дифференциальных уравнений, используя для их решения средства пакета MathCAD.

Содержание работы:

1) изучить теоретические положения (раздел 3.1), определяющие структуру динамических объектов, их математическое описание и решение задачи анализа объектов, методы решения обыкновенных дифференциальных уравнений и систем уравнений;

2) выполнить индивидуальное задание согласно предусмотренной в разд.3.2 последовательности выполнения работы;

3) оформить описание контрольной работы согласно требованиям задания.

3.1. Краткие теоретические положения

3.1.1. Структура и математическая модель объекта

В общем случае под динамическими (нестационарными) объектами понимают такие объекты, состояние и поведение которых определяется временными характеристиками, т.е. является функцией времени.

Такого рода объекты могут быть описаны системами нелинейных дифференциальных уравнений вида

где – функционал, определяющий конкретный вид системы уравнений, которая описывает структуру объекта; – вектор переменных, описывающий выходы объекта; – вектор производных; – вектор внутренних параметров уравнения, определяющий конкретную реализацию объекта при заданной его структуре; – внешние (входные) воздействия на объект.

 Скачать реферат