Эмисионная электроника

m= – e (uz Bx – ux Bz );

m=– –e (ux By – uy Bx ),

или с учетом условий

Bx =Bz =0, а Ву = – В:

m= e B uz;

m= 0;

m=e Bux.

Интегрирование второго уравнения системы с учетом начального условия: при t=0, uy=uyo приводит к соотношению:

т.е. показывает, что магнитное поле не влияет на компоненту скорости электрона в направлении силовых линий поля.

Совместное решение первого и третьего уравнений системы, состоящее в дифференцировании первого по времени и подстановке значения duz /dt из третьего, приводит к уравнению, связывающему скорость электрона ux cо временем:

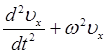= 0,

где

Решение уравнений такого типа можно представить в виде:

ux = A cosw t + C sinw t,

причем из начальных условий при t=0, ux = uxo , dux /dt = 0 (что следует из первого уравнения системы, так как uzo = 0 ) вытекает, что

ux = uxo × cos w t.

Кроме того, дифференцирование этого уравнения с учетом первого уравнения системы приводит к выражению:

uz =uxo× sinw t.

Заметим, что возведение в квадрат и сложение двух последних уравнений дает выражение:

ux2 + uz2= uxo2 = const,

которое еще раз подтверждает, что магнитное поле не изменяет величины полной скорости (энергии) электрона.

В результате интегрирования уравнения, определяющего его ux, получаем:

x =× sin w t,

постоянная интегрирования в соответствии с начальными условиями равна нулю.

Интегрирование уравнения, определяющего скорость uz с учетом того, что при z = 0, t=0 позволяет найти зависимость от времени координаты Z электрона:

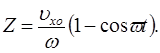
Решая два последних уравнения относительно sinwt и coswt, возводя в квадрат и складывая, после несложных преобразований получаем уравнение проекции траектории электрона на плоскости XOZ:

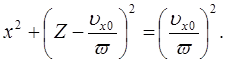
Это уравнение окружности радиуса

r =/ w

центр которой расположен на оси z на расстоянии r от начала координат (рис. 3.2). Сама траектория электрона представляет собой цилиндрическую спираль радиуса

c шагом .

Из полученных уравнений очевидно также, что величина

представляет собой круговую частоту движения электрона по этой траектории.

Вопрос 14: Электрический ток в вакууме при наличии объемного заряда

До сих пор рассматривались закономерности движения электронов в вакууме, когда объемный заряд незначительный, картина электрического поля описывается уравнением Лапласа.

Однако в большинстве приборов используются значительные токи и формируются объемные заряды такой плотности, что ими нельзя пренебрегать.

Различают два режима: режим пространственного заряда и насыщения.

Рассмотрим закономерности режима пространственного заряда.

Представим анод и катод в виде плоскостей. На рис. 3.3 по оси абсцисс отложено расстояние от катода до анода, вверх от нулевой линии – положительное напряжение, вниз – отрицательное. Допустим, что из катода выходит определенное количество электронов и величина эта постоянная

()

Если на анод не подано напряжение, то электроны, выйдя из катода, хаотически двигаются в диодном промежутке, образуя между катодом и анодом отрицательный объемный заряд (кривая 1).

Подадим на анод небольшое положительное напряжение. Электроны ускоряются анодом, в цепи анода протекает ток, но он меньше, чем ток эмиссии

()

Распределение потенциала между электродами при этом показано кривой 2. Отрицательный объемный заряд сохраняется только у катода, при этом образуется потенциальный минимум . Электрон, выйдя из катода, попадает в тормозящее поле этого потенциала, и только если его энергия больше , преодолевает этот потенциальный барьер и ускоряется полем анода:

Если энергия у электрона меньше, он не может преодолеть этот барьер и остается в области отрицательного пространственного заряда. Диодный промежуток в этом случае работает в режиме ограничения анодного тока объемным пространственным зарядом.

Зависимость анодного тока от напряжения на аноде определяется уравнением:

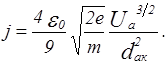
Подставив постоянные, получим:

(А/см2),

где – выражено в вольтах;

– в см

Это выражение носит название закона степени трех вторых. Если плотность тока анода умножить на площадь анода, получим ток анода

Уравнение степени трех вторых описывает диодную характеристику, представленную на рис.3.4. Закон степени 3/2 применим в любом электронном, вакуумном приборе при наличии объемного пространственного отрицательного заряда у катода

 Скачать реферат