Эмисионная электроника

Коэффициент ионно-электронной эмиссии g представляет отношение вторичного электронного тока Ie2 к ионному току (Ii ), зависит от материала кристалла, рода бомбардирующих ионов и их кинетической энергии. При энергиях порядка десятков и сотен электронвольт значения g лежат в пределах 10–3¸10–1. С увеличением энергии ионов этот коэффициент возрастает и при энергиях в несколько тысяч электрон

вольт может стать больше единицы.

Эксперименты показывают, что существуют два разных процесса выбивания вторичных электронов ионами. Выбивание электронов ионами за счет кинетической энергии последних называется кинетическим вырыванием. Вырывание электронов ионами за счет энергии, высвобождающейся при рекомбинации на поверхности кристалла или вблизи ее, называют потенциальным вырыванием.

Кинетическое вырывание: при столкновении иона с атомом кристалла происходит «встряска» их электронных оболочек, в результате которой может освободиться электрон с достаточно большой для преодоления потенциального барьера энергией, или это результат ионизации поверхностного слоя атомов кристалла ударами ионов.

При потенциальном вырывании положительный ион подходит к поверхности кристалла, при этом потенциальный барьер между ними будет снижаться и сужаться, и станет возможным переход одного из наиболее быстрых валентных электронов кристалла к иону.

Вторичная ионно-электронная эмиссия наблюдается в условиях электрического разряда в газах.

ТОКОПРОХОЖДЕНИЕ В ВАКУУМЕ

Вопрос 12: Движение электронов в вакууме в электрическом и магнитных полях

В электрическом поле напряженностью Е на электрон действует сила

противоположная по направлению вектору Е.

В магнитном поле с индукцией В на движущийся электрон действует сила Лоренца. При произвольной ориентации векторов эту силу удобно представить в векторной форме:

где – вектор скорости электрона.

При наличии электрического и магнитного полей действующая на электрон сила:

Поскольку при движении в вакууме электрон не испытывает столкновений, приводящих к изменению величины и направления его скорости, получаем уравнение движения электрона

Это уравнение позволяет полностью описать движение электрона, найти его траекторию и скорость в любой точке, если известны начальные условия: координаты, величина и направление скорости в начале пути и, главное, если известна картина поля, т.е. заданы в виде функции координат векторы напряженности электрического поля и магнитной индукции .

Нахождение картины поля является первым этапом решения задач о движении электронов в межэлектродном пространстве.

Аналитически картину электрического поля в пространстве, свободном от зарядов, можно найти решением уравнения Лапласа:

Это для случая малых потоков или единичных электронов.

В случаях, когда электроны и другие заряженные частицы находятся в межэлектродном пространстве в большом количестве и влияют на картину электрического поля, в основу расчета должно быть положено уравнение Пуассона:

где – плотность объемного заряда;

– диэлектрическая проницаемость.

Однако картины электрического поля аналитическим путем можно найти для простых конфигураций электродов, а для сложных электродов используют эксперимент (электрическая ванна, метод сеток, метод сопротивлений) или приближенные методы расчета.

Картину магнитного поля также можно получить аналитически только для простейших случаев.

Вернемся к уравнению:

Умножив левую и правую части скалярно на скорость электрона , получим

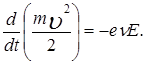
Второе слагаемое равено нулю потому, что сила Лоренца перпендикулярна направлению движения электрона.

Выясняется, что под действием магнитного поля изменяется только направление движения электрона, а его скорость не меняется по величине.

Электрическое поле влияет на кинетическую энергию и на направление движения.

Уравнение, связывающее энергию свободного электрона с пройденной разностью потенциалов U:

Если начальную энергию электрона охарактеризовать некоторой разностью потенциалов U0 , т.е. выразить ее в электрон-вольтах, то скорость электрона, прошедшего разность потенциалов U

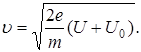
Напомним, что при скоростях электрона, близких к скорости света, во всех приведенных уравнениях должна быть релятивистская масса электрона. Однако, как показывает расчет, релятивистский эффект учитывается только при анализе движения электрона, ускоряемого разностью потенциалов в несколько десятков киловольт. Поэтому далее будем считать массу электрона постоянной.

Вопрос 10: Движение электрона в однородном электрическом поле

Электроды плоскопараллельны на расстоянии d один от другого (рис. 3.1).

Уравнение Лапласа, имеющее вид

после интегрирования сводится к уравнению

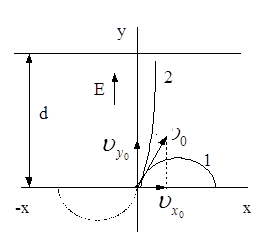
Рис. 3.1 – Движение электрона в однородном электрическом поле

Уравнение движения электрона в прямоугольной системе координат разбивается на три уравнения:

В рассматриваемом случае магнитное поле отсутствует, а электрическое имеет одну компоненту . Тогда система уравнений запишется как

Пусть в момент электрон находится в точке начала координат и движется со скоростью ««, имеющей компоненты по осям х и y, а компонента скорости по z равна нулю. Тогда интегрирование приводит к уравнениям:

После повторного интегрирования первых двух уравнений получаем

Константы интегрирования в обоих случаях равны нулю, поскольку в начальный момент

интегрирование третьего уравнения дает

Исключим :

.

Получим уравнение траектории электрона:

Видно, что движение происходит по параболе (кривая 1 на рис. 3.1), обращенной выпуклостью вверх. Анализ показывает, что вершина этой параболы имеет координаты

Совершая движение по этой траектории, электрон возвращается к оси х в точке с координатой:

Если вектор напряженности поля направить в противоположную сторону то изменяется знак первого члена уравнения траектории электрона:

т.е. в данном случае электрон будет двигаться по траектории 2 (на рис. 3.1). Это отрезок параболы, симметричный относительно начала координат параболе 1.

Вопрос 11: Движение электрона в однородном магнитном поле

Для решения этой задачи так же воспользуемся прямоугольной системой координат. Ось у направим навстречу вектору магнитной индукции В, а ось x – так, чтобы вектор скорости электрона u, находящегося в момент времени t = 0 в точке начала координат, лежал в плоскости XOY, т.е. имеем компоненты uxo и uyo.

В отсутствии электрического поля система уравнений движения электрона принимает вид:

m= – е ( uу × Вz – uz By );

 Скачать реферат