Электродинамические усилия в электрических аппаратах

Тогда

(30)

т.е. результат, как и следовало, получился тот же.

Для двух параллельных проводников, расположенных с любым сдвигом, Г.Б. Холявский получил удобную для расчета коэффициента контура формулу, основанную на геометрической интерпретации приве

денных выше уравнений.

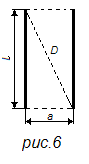
Величина представляет собой длину диагонали D (рис. 6) прямоугольника со сторонами l и а; следовательно, согласно уравнению (20) для проводников равной длины

(31a)

а согласно уравнению (25) для проводников неравной длины (рис. 7)

(31б)

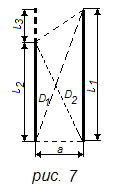
т.е. коэффициент контура равен разности суммарных диагоналей и боковых сторон четырехугольника (прямоугольник, трапеция, параллелограмм), построенного на данных отрезках проводников, деленной на его высоту.

Для проводников прямоугольного сечения (шин) следует вводить поправочный коэффициент — коэффициент формы kф, зависящий от размеров проводников и расстояний между ними:

(32)

4. Электродинамические силы между взаимно перпендикулярными проводниками

На рис. 8 и 9 приведены часто встречающиеся в аппаратах формы перпендикулярно расположенных проводников, например в рубильниках, мостиковых контактных системах и многих других аппаратах и узлах. Произведя расчеты, аналогичные предыдущим (первый метод), получим следующие выражения для сил, действующих на проводник 1 по рис.8 при h →∞

(33)

и при h конечном

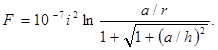(34)

по рис. 9 сила будет соответственно в два раза большей:

(35)

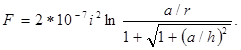(36)

Моменты относительно точки О, действующие на проводник 1 (h →∞), по рис. 8:

(37)

(38)

Момент относительно точки О, действующий на половину проводника 1 (рис. 9),

(39)

5. Электродинамические силы в кольцевом витке и между кольцевыми витками

Для одного витка

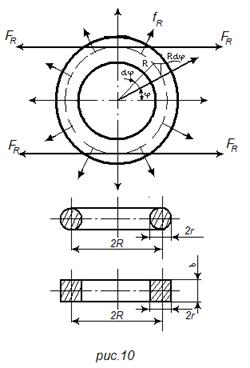
В кольцевом витке (рис. 10) с током i возникают радиальные силы fR, стремящиеся увеличить его периметр, т.е. разорвать виток. Если считать, что сечение проводника не деформируется, то согласно выражению (13) общая радиальная сила, действующая на виток, будет

(40)

На единицу длины витка приходится сила

(41)

Для того чтобы найти силу FR, стремящуюся разорвать виток, необходимо проинтегрировать проекции радиальных сил, действующих на четверти витка. На элемент окружности витка Rdφ действует сила fRRdφ, проекция которой на ось х равна fRRdφ cos φ, откуда

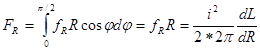(42)

Для витка круглого сечения при R >> r

(43)

и

(44)

Аналогично для витка прямоугольного сечения

(45)

и

(46)

Для нескольких витков

Приведенные формулы для электродинамических сил применимы не только к одному витку, но и к обмоткам с любым числом витков п, занимающим данное сечение. В этом случае за значение тока следует принимать суммарное значение тока всех витков i =niв.

В катушках аппаратов, кроме сил, действующих внутри каждого витка, будут существовать электродинамические силы между витками. Между витками (рис. 11а), если считать, что токи в них направлены одинаково, возникает сила притяжения F. Силу F можно представить как результирующую двух составляющих, а именно силы Fy, стремящейся притянуть витки друг к другу, и силы Fx, стремящейся один из витков (при одинаково направленных токах — виток с меньшим диаметром) растянуть, а другой виток (в данном случае виток большего диаметра) — сжать. Таким образом, в одном из витков сила Fx будет складываться с силой FR, а в другом — вычитаться из нее.

Значения составляющих силы взаимодействия между двумя витками определяются уравнениями:

(47)

(48)

где c = R2-R1; R2> R1. Зависимости Fx и Fy от расстояния между витками представлены на рис. 11, б и в.

6. Электродинамические силы в проводниках переменного сечения

В проводнике силы взаимодействия отдельных линий тока с собственным магнитным полем проводника направлены перпендикулярно линиям тока. При неизменном сечении проводника все линии тока параллельны и силы не имеют осевой составляющей (в цилиндрическом проводнике они направлены по радиусу: F = Fr на рис. 12).

При изменении сечения проводника линии тока искривляются, и кроме поперечной Fr появляется продольная составляющая Fl стремящаяся разорвать место перехода вдоль оси проводника. Эта сила всегда направлена в сторону большего сечения и равна

(49)

Формула справедлива для любого перехода.

7. Силы взаимодействия между проводником с током и ферромагнитной массой

Вблизи ферромагнитной массы

Вблизи ферромагнитной массы магнитное поле вокруг проводника с током (рис 13) искажается, магнитные силовые линии стремятся замкнуться по массе и возникают силы, стремящиеся притянуть проводник к этой массе.

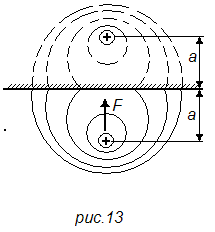
Значение силы притяжения может быть определено из следующих соображений. Заменим ферромагнитную массу вторым проводником с током того же направления, расположенным на таком же расстоянии от границы раздела сред. Картина поля при этом не нарушится, так как одновременно с удвоением длины магнитной силовой линии удвоилась и магнитодвижущая сила (2i вместо i), т.е. такая замена вполне правомерна. Силы взаимодействия между двумя параллельными проводниками подсчитываются по уравнениям (19) и (20). Только в данном случае вместо расстояния а надо брать 2а, т.е.

 Скачать реферат