Имитационная модель динамики численности русского осетра

20. Мухачев И.С. Озерное рыбоводство. М., 1989.- 98с.

21. Никоноров А.М., Хоружая Т.А., Бражникова Л.В., Жулидов А.В. Мониторинг качества вод: оценка токсичности. С.-Петербург. Гидрометеоиздат. 2000. 150 с

22. Никольский Г.В. Экология рыб. М., 1974. – 47с.

23. Привезенцев Ю.А. Использование теплых вод для разведения рыбы. М.,1986.999.- С. 25-32.

24. Ходоревская, RP, Е. В. Красик

ов, Ф. Довгопол и О. Журавлева, Ихтиологический мониторинг состояния осетра в Каспийском море. В: мониторинге биоразнообразия. Москва. 1997. 159-164.

ПРИЛОЖЕНИЕ

Корреляционно-регрессионный анализ

Построим график, отложив вдоль оси абсцисс содержание х, а вдоль оси ординат- у. Тогда каждой паре значений х и у на графике будет соответствовать определенная точка. По характеру расположения точек можно предположить существование нелинейной функции между х и у.

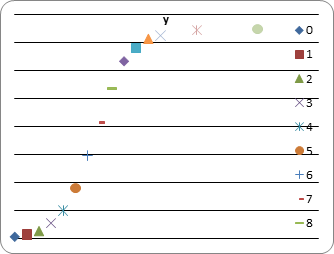
Рис.1 График экспериментальных данных

Из данного графика мы можем определить, что приведенное уравнение является логистическим уравнением Ферхюльста(1838), описывающим рост популяции в условиях внутривидовой конкуренции.

Если δ- коэффициент пропорциональности;

У - численность популяции в момент х;

r - коэффициент роста;

К - предельная плотность популяции

начальное условие: при х=0 численность особей у=

отсюда логистическое уравнение:

При х=1; у=30; =14;К=1499 (из данного графика):

Рис.2 График теоретической зависимости

Остаточная дисперсия:

 Скачать реферат