Формирование рыночных равновесных цен

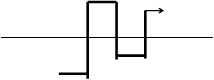
Рис. 12. Блок-схема паутинообразной модели А

3) потребитель предъявляет спрос, который при цене Pt+1 в каждый момент времени равен предложению St+1, вследствие чего потребитель приобретает все, что ему предложено.

Принятое в модели А взаимодействие подсистем “потребитель”, “товаропроизводитель” и

“рынок” может быть представлено в виде блок-схемы, изображенной на рис.12.

Использование монотонных функций спроса и предложения позволяет построить последовательность цен Pt, где t — номер шага во времени. Действительно, в силу гипотезы (1) товаропроизводитель по значению цены P1 при помощи кривой предложения определяет S2; в силу гипотезы (2) на рынке устанавливается цена P2 (находится при помощи кривой спроса); в силу гипотезы (3) весь товар в количестве S2 находит потребителя; в силу гипотезы (1) товаропроизводитель, ориентируясь на цену P2, определяет объем предложения S3 и т.д. (рис.12). Далее рассмотренный процесс повторяется.

Ц е н а P S D Количество товара

P t

Рис. 13 Паутинообразная модель А при s<d.

Таким образом, сформулированные две гипотезы приводят к итерационному процессу (4), где спрос запаздывает от предложения на один период.

Динамика цены (а также спроса и предложения) в рамках данной модели может быть изображена в виде кривой, которую называют либо паутиной, либо спиралью (рис.13). Поэтому в литературе паутинообразную модель иногда называют “динамической спиралью”. В случае, изображенном на рис.13, последовательность цен Pt стремится к равновесному уровню pe, и, таким образом, здесь со временем устанавливается равновесие.

Для ответа на вопрос, всегда ли в данной модели итерационный процесс (4) приводит к равновесию, рассмотрим случай, когда функции спроса и предложения линейно зависят от цены, т.е.

D(P)=Qe-d(P-pe), S(P)=Qe+s(P-pe). (5)

Здесь pe — равновесное значение цены; Qe — соответствующее равновесное значение спроса и предложения; d и s — угловые коэффициенты функций спроса и предложения.

В силу уравнений (5) итерационный процесс (4) может быть представлен в виде

Qe-d(Pt+1-pe)=Qe+s(Pt-pe),

или

Pt+1-pe=-s(Pt-pe)/d.

Это значит, что числовая последовательность yt=Pt-pe, которая определяет отклонение текущей цены от равновесной, представляет собой знакочередующуюся геометрическую прогрессию

yt+1=qyt (6)

Ц е н а P S D Количество товара

 Скачать реферат