Структурный синтез устройств с мультидифференциальными операционными усилителями

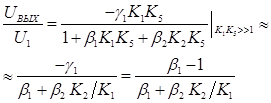(11)

(12)

где ; ; Ki – коэффициент передачи соответствующего плеча дифференциального каскада (рис. 1б).

При условии,

что все Ki равны по абсолютной величине, что легко выполнимо, выражения (11) и (12) можно представить как

; (13)

. (14)

Для неинвертирующего включения мультидифференциального ОУ по каждому из неинвертирующих входов коэффициент передачи можно представить как

(15)

(16)

Из выражений (11)–(16) следует, что при использовании многоконтурных ООС глубина обратной связи возрастает, в частности, в классическом ОУ для неинвертирующего включения при = 0,5 коэффициент усиления будет близок к двум, а в рассматриваемом случае при 1 = 2 = = 0,5 коэффициент усиления будет близок к единице.

Очевидно, что при одновременном использовании инвертирующих и неинвертирующих входов выходное напряжение ОУ можно определить согласно принципу суперпозиции, если сопротивление источников сигналов будет много меньше входных сопротивлений соответствующих входов.

Поскольку коэффициенты Кi– комплексные и, в общем случае, постоянные времени высоких частот каждого дифференциального каскада различны, передаточная функция для случая неинвертирующего включения ОУ будет иметь вид:

(17)

поэтому обеспечение устойчивости такого усилителя может оказаться сложной, но решаемой задачей.

Ток потребления стандартного ОУ складывается из следующих составляющих (если входной одиночный дифференциальный каскад выполнен аналогично рис. 2):

IОУ = IВК + I1 + 2I0 » 2I1 + 2I0, (18)

где IВК, I1, 2I0– токи, потребляемые выходным, промежуточным и входным дифференциальным каскадами.

Для схем мультидифференциальных ОУ, представленных на рис. 2 и 4 соответственно

IОУ = IВК + 2I1 + 4I0, (19)

IОУ = IВК + 2I1 + 6I0, (20)

откуда следует, что ток МОУ возрастает весьма незначительно по сравнению с классическим.

3. Обобщенная структура и основные свойства электронных схем с мультидифференциальными ОУ

Увеличение числа входов дифференциальных каскадов, как это было показано ранее, приводит к снижению коэффициента ослабления синфазного сигнала, причем он может зависеть от требуемого количества входов. Кроме этого, необходим поиск особенностей функционально-топологиче-ских принципов введения в схему дополнительных (компенсирующих) обратных связей и, следовательно, анализ основных свойств электронных схем с МОУ.

Для решения поставленной задачи воспользуемся обобщенной структурой электронных схем с МОУ (рис. 5).

Рис. 5. Обобщенная структура с мультидифференциальными ОУ

Из векторного сигнального графа (рис. 6) этой структуры следует система векторно-матричных уравнений:

(21)

Смысл векторов следует из рис. 6. Векторы , размерностью N´1 описывают расщепитель входного сигнала x0 и связывают его с инвертирующим (-) и неинвертирующим (+) входами мультидифференциальных ОУ . Матрицы , образованы локальными пе-редаточными функциями пассивной подсхемы, обеспечивающей передачу и преобразование сигнала со входа i-го активного элемента на j-й инвертирующий или неинвертирующий входы l-го МОУ. Активные элементы описываются диагональными матрицами размера (N´N):

, (22)

компоненты которых являются передаточными функциями i-го МОУ по j-му инвертирующему (-) и неинвертирующему (+) входам.

Рис. 6. Векторный сигнальный граф обобщенной структуры

Связь выходов активных элементов с нагрузкой осуществляется через сумматор, локальные передачи которого образуют вектор T = [ti] размера (N´1). Для учета влияния ослабления синфазного сигнала по различным входам введем в общем случае функции:

, (23)

характеризующих неидентичность каналов усиления входного сигнала. Тогда

(24)

(25)

Решение системы (21) приводит к следующему вектору выходных сигналов МОУ:

, (26)

где (27)

; (28)

; (29)

. (30)

Из (26) может быть получена передаточная функция любого электронного устройства с МОУ:

. (31)

Реально коэффициенты ослабления синфазного сигнала достаточно велики, поэтому при анализе их влияния на функцию (31) можно исключить мультипликативные составляющие, представляющие собой величины второго порядка малости.

Рассмотрим влияние j-го коэффициента для инвертирующего входа i-го активного элемента. Индекс j соответствует номеру матрицы:

. (32)

Тогда по методу Дуайра и У0 [2] (метода пополнения при обращении матрицы) получим:

, (33)

где .

Следовательно,

. (34)

В выражении (34)

(35)

является локальной передаточной функцией системы при подаче сигнала на j-й вход i-го активного элемента, представляет собой передаточную функцию при условии, что вектор Т образован компонентами i-й строки матрицы , а

 Скачать реферат