Оптимизация организационных решений

Данный план распределения продукции является наиболее эффективным из представленных, хотя не до конца оптимальным.

Вывод

Поскольку в оптимальном плане прирост мощности 40 тыс. у. е. продукции за счет строительства отнесен на фиктивного потребителя, то строительство нового цеха или пристройку цеха к действующему следует считать нецелесообразным, и капитальные вложения необходимо направить на реконструкцию действующего предприятия.

Задание №2

Применение симплекс-метода для оптимальной организации

ремонтно-строительных работ

Определить максимальное количество квартир в домах кирпичных и крупнопанельных, которые можно отремонтировать из имеющихся ресурсов.

Решение

Для решения данной задачи применим симплекс-метод.

Обозначим:

Х1 – искомое количество квартир в кирпичном доме;

Х2 – искомое количество квартир в панельном доме.

Целевая функция:

L = Х1 + Х2 max

Ограничениями будут неравенства, полученные на основании исходных данных:

1. Арматура 0,6Х1 + 1,3 Х2 ≤ 900;

2. Пиломатериалы 0,8Х1 + 0,3 Х2 ≤ 520;

3. Цемент 5Х1 + 9Х2 ≤ 7 000;

4. Керамическая плитка 0,5Х1 ≤ 400;

5. Трудозатраты 70Х1 + 50Х2 ≤ 55 000;

6. Х1 ≥ 0;

7. Х2 ≥ 0.

Поскольку имеется только два неизвестных, то применим геометрическое решение. Для удобства построений преобразуем не равенства.

1. 6Х1 + 13 Х2 ≤ 9 000;

2. 8Х1 + 3 Х2 ≤ 5 200;

3. 5Х1 + 9Х2 ≤ 7 000;

4. 5Х1 ≤ 4 000;

5. 7Х1 + 5Х2 ≤ 5 500;

6. Х1 ≥ 0;

7. Х2 ≥ 0.

Геометрически ограничения неравенств выражаются в виде открытых полуплоскостей, ограниченных осями координат и линиями, описываемыми равенствами, полученными из выражений ограничений:

1. 6Х1 + 13 Х2 = 9 000;

2. 8Х1 + 3 Х2 = 5 200;

3. 5Х1 + 9Х2 = 7 000;

4. 5Х1 = 4 000;

5. 7Х1 + 5Х2 = 5 500.

Нанесем эти линии на график.

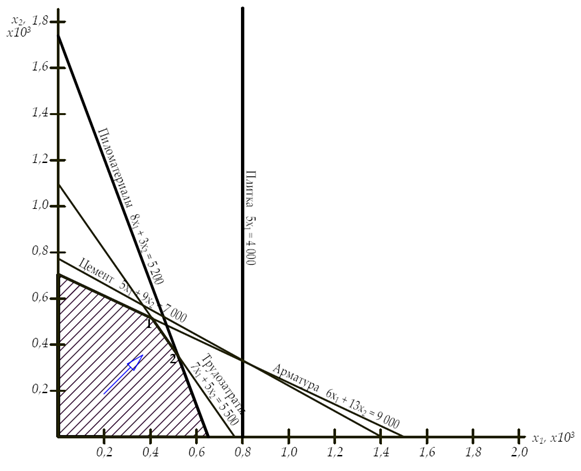
В целом условиям неравенств удовлетворяет заштрихованная область. Оптимальное решение находится на контуре этой фигуры в одной из узловых точек и определяется совместным рассмотрением выражений:

L = Х1 + Х2 max

6Х1 + 13 Х2 = 9 000;

8Х1 + 3 Х2 = 5 200;

5Х1 + 9Х2 = 7 000;

5Х1 = 4 000;

7Х1 + 5Х2 = 5 500.

Возрастание целевой функции направлено слева вверх под углом 45°, и последней точкой в допустимой области будет точка 1 или 2.

Точка 1 получена пересечением прямых, описываемых равенствами:

6Х1 + 13 Х2 = 9 000;

7Х1 + 5Х2 = 5 500.

Решая эти равенства, найдем координаты точки 1: Х1 = 200; Х2 = 600.

Аналогично найдем координаты точки 2 из выражений:

7Х1 + 5Х2 = 5 500;

8Х1 + 3 Х2 = 5 200.

Координаты точки 2: Х1 = 498; Х2 = 406.

Найдем, какая из указанных точек дает большее значение целевой функции.

L1 = Х1 + Х2 = 200 + 600 = 800;

L2 = Х1 + Х2 = 498 + 406 = 904.

Оптимальной является точка 2, дающая 498 квартир в кирпичных домах и 406 в панельных. При этом будут полностью исчерпаны такие ресурсы как пиломатериалы и трудозатраты.

Использование остальных ресурсов найдем, решая вышеуказанные равенства при зафиксированных значениях Х1 = 498; Х2 = 406.

0,6 х 498 + 1,3 х 406 = 299 + 528 = 827 (арматура), неиспользовано 73 т арматуры.

5 х 498 + 9 х 406 = 2 490 + 3 654 = 6 144 (цемент), неиспользовано 856 т.

0,5 х 498 = 249 тыс. шт. (керамическая плитка), неиспользовано 151 тыс. шт.

Полученные результаты занесем в таблицу:

 Скачать реферат