Оптимизация организационных решений

Вывод: Максимальное количество домов, которые можно отремонтировать, используя данные ресурсы – 498 шт. (кирпичные) и 406 шт. (панельные). При ремонте пиломатериалы и трудозатраты используются полностью, остальные ресурсы – с остатком.

Задание №3

Применение методов динамического программирования

(принципа оптимальности Р. Беллмана)

при календарном

планировании в строительстве

Выбрать такую очередность включения объектов в строительный поток, чтобы длина суммарного пути перебазирования оказалась минимальной.

Исходные данные – расстояние между пунктами, км

Составим таблицу вариантов, состоящих лишь из трех участков перебазирования. Сгруппируем эти варианты по одинаковым объектам, стоящим на последнем месте.

Из каждой пары вариантов выберем наиболее перспективные (с меньшим значением). Затем развиваем и сопоставляем лишь перспективные варианты.

Составляем таблицу, в которую внесем перспективные варианты из предыдущей таблицы и добавим к каждому из них А0 (возвращение мехколонны на исходную базу).

Таким образом, устанавливаем, что есть два равноценных оптимальных варианта последовательности строительства объектов.

Задание №4

Оптимизация очередности строительства объектов

в неритмичных потоках

Определить оптимальную очередность строительства нескольких объектов, при которой достигается минимальная общая продолжительность строительства, а также величину общей продолжительности строительства при исходной и оптимальной очередности строительства объектов.

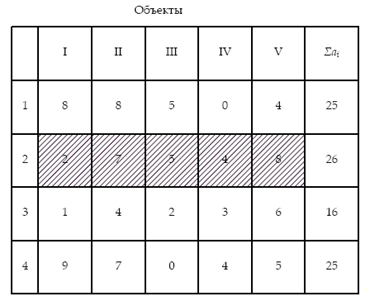
Выделяем поток №3 как поток наибольшей продолжительности. Затем по каждому объекту находим общее рабочее время, предшествующее потоку наибольшей продолжительности и общее рабочее время, последующее за потоком наибольшей продолжительности.

В третью строку под матрицей записываем со своим знаком разницу между продолжительностью работы на данном объекте последней и первой бригад.

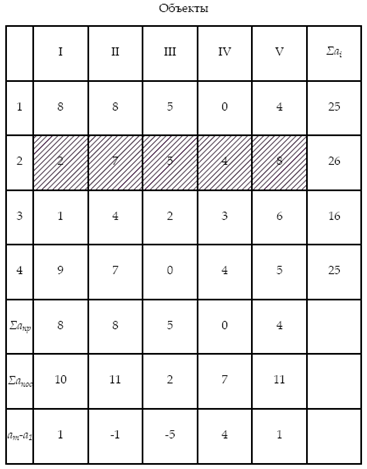
На основе данных дополнительных строк устанавливается рациональная очередность строительства объектов из следующих соображений:

а) на первом месте располагается объект с наибольшим значением Σапос. Остальные объекты располагаются так, чтобы Σапр постепенно возрастало, а Σапос снижалась к концу матрицы;

 Скачать реферат