Математический расчет объема выпуска продукции

Находим пробное решение, для этого все свободные переменные приравниваем к 0, а базисные к bi

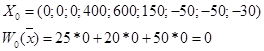
Решение пробное.

Но так как в столбце bi есть отрицательные коэффициенты, то решение не ОПОРНОЕ.

Для решение задачи двойственным симплекс методом для начала необходимо добиться, что б решение было ОПОРНЫМ.

Находим в столбце Bi минимальный отрицательный коэффициент.

Bi=min{bi<0}=min{-50;-50;-30}= -50

Соответствует сразу двум строкам А7 и А8. Одна из этих строк будет разрешающей.

Для того что б определиться какую из двух строк выбрать в качестве разрешающей, для каждой найдем разрешающий столбец, а затем проверим при замене какой пары (разрешающая строка + разрешающий столбец) изменение функции цели будет больше (ту пару и будем менять)

1) А7- разрешающая строка

Ищем разрешающий столбец по правилу:

(так как среди оценочной строки имеются отрицательные оценки плана (задача максимизации), то среди отрицательных коэффициентов аij разрешающей строки выбирается разрешающий элемент аrs для которого

соответствует столбцу А1

Если заменим А1—А7 то функция цели изменится на:

2) А8- разрешающая строка

соответствует столбцу А2

Если заменим А2—А8 то функция цели изменится на:

В первом случае изменение функции больше, поэтому выбираем пару А1-А7 меняем вектора местами и переходим к новой симплекс-таблице по правилу:

Переходим к новой симплекс таблице по следующему правилу:

1. все элементы разрешающей строки делим на разрешающий элемент

2. заполняем базисные столбцы

3. все остальные элементы симплекс таблицы находим по формуле:

 Скачать реферат