Уравнения и характеристики распространения волн реального электромагнитного поля

Обсудим характеристики распространения ЭМ поля в виде плоской линейно поляризованной волны в однородной изотропной материальной среде. С точки зрения большей общности при анализе характеристик распространения указанного поля обычно значительно удобней использовать не волновые уравнения, а напрямую – сами уравнения системы (1), являющиеся по сути дела первичными уравнениями ЭМ волны. Для этого р

ассмотрим пакет указанной волны, распространяющийся вдоль оси x с компонентами и , которые представим комплексными спектральными интегралами:

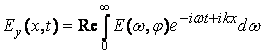и ,

где и – комплексные амплитуды. Подставляя их в уравнения Максвелла (1a) и (1c), приходим к соотношениям и . В итоге получаем для уравнений системы (1) выражение: .

В конкретном случае среды идеального диэлектрика () с учетом формулы из следует обычное дисперсионное соотношение [2], описывающее однородные плоские волны ЭМ поля. При этом связь комплексных амплитуд в волновых решениях системы уравнений (1) представится в виде , а сами решения описывают волну, полевые компоненты и которой синфазно () распространяются в пространстве.

Поскольку суть электромагнетизма – это взаимодействие ЭМ поля с материальной средой, то его анализ обычно сводится к стремлению описать энергетику ЭМ явлений. Обратимся и мы к соотношению энергетического баланса (2), которое для среды идеального диэлектрика запишется в виде:

. (3)

Для анализа нам вполне достаточно рассмотреть, как выполняется выражение (3) для плоской монохроматической ЭМ волны, полевые компоненты которой, согласно волновым решениям уравнений Максвелла, в свободном пространстве без потерь при распространении совершают синфазные колебания: и . Подставляя эти выражения в соотношение (3), окончательно получаем:

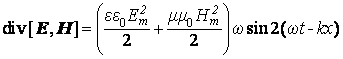. (4)

Здесь весьма странно то, что, согласно , равные по величине электрическая и магнитная энергии хотя и распространяются совместно, но без видимой связи друг с другом. Кстати, в случае электро- и магнитостатики эти энергии в принципе раздельны и независимы. Таким образом, необходимо напрашивается вывод об объективности существования чисто электрической и магнитной энергий, при отсутствии каких-либо оснований считать, что распространение ЭМ волны реализуется посредством взаимной перекачки одной энергии в другую. Но тогда становится совершенно неясным, что же такое, казалось бы, очевидное для каждого понятие ЭМ энергии, а также каков реальный механизм волнового переноса всех этих видов энергии.

Итак, решение уравнений электродинамики Максвелла для ЭМ волны не отвечает обычным физическим представлениям о распространении энергии посредством волн в виде процесса взаимного преобразования во времени в данной точке пространства энергии одной компоненты поля в энергию другой его компоненты. Следовательно, электродинамические уравнения (1) описывают необычную, весьма странную волну, которую логично назвать псевдоволной, поскольку, с одной стороны, синфазные компоненты волны в принципе не способны переносить энергию, а с другой – перенос ЭМ энергии реально наблюдается, более того, это явление широко и всесторонне используется на практике, определяя многие аспекты жизни современного общества.

Таким образом, имеем парадокс, существующий, как это ни странно, уже более века. Поражает здесь то, что традиционная логика обсуждения переноса ЭМ энергии такова, что проблемы как бы и нет, всем все понятно. И действительно, из соотношения для амплитуд в волновых решениях уравнений системы (1) формально следует закон сохранения энергии , хотя, как установлено выше, синфазные волны энергетически несостоятельны. Правда, изредка делаются попытки аргументировано разобраться в этом вопросе, но эти объяснения (например, [3]), на наш взгляд, не выдерживают критики, поскольку обсуждаются не сами уравнения Максвелла или их прямые следствия, а то, что эти уравнения не учитывают характеристики реальных ЭМ излучателей или некую специфику взаимодействия материальной среды с ЭМ полем. По мнению авторов, это и создает сдвиг фазы колебаний между компонентами на , реализующий перенос ЭМ энергии.

В этой связи напомним основные физические представления о переносе энергии посредством волнового процесса, например, рассмотрим распространение волн от брошенного в воду камня. Частицы воды массой , поднятые на гребне волны на высоту , имеют запас потенциальной энергии , а через четверть периода колебаний, когда гребень волны в данной точке пространства спадет, в соответствии с законом сохранения энергии, потенциальная энергия частиц воды перейдет в кинетическую энергию их движения , где скорость частиц . Наличие взаимодействия молекул воды и приводит к возбуждению механической поверхностной поперечной волны, которая переносит в волновом процессе механическую энергию так, что . Физически логично считать, что механизм переноса энергии ЭМ волнами в главном должен быть аналогичен, как и у других волн иной физической природы, возможно обладая при этом, исходя из структуры электродинамических уравнений Максвелла (1), определенной спецификой и даже уникальностью.

 Скачать реферат