Принципы томографии

Спиновые пакеты

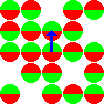
Весьма обременительным является описание ЯМР на микроскопическом уровне. Макроскопическая картина более удобна. Первым шагом к созданию макроскопической картины определим спиновый пакет. Спиновый пакет - это группа спинов испытывающих на себе одну и ту же силу магнитного поля. В этом примере, спины внутри каждой секции решетки представляют собой спиновый пакет. В любо

й момент времени магнитное поле, соответствующее спинам в каждом спиновом пакете может быть представлено вектором намагниченности.

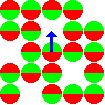
Величина каждого вектора пропорциональна (N+ - N-).

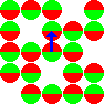
Сумма всех векторов намагниченности всех спиновых пакетов является суммарной (общей) намагниченностью. Для описания импульсного ЯМР необходимо пользоваться термином суммарной намагниченности.

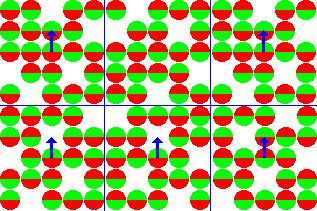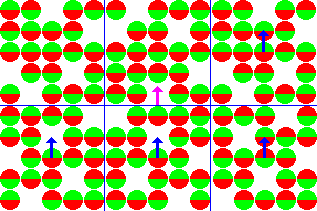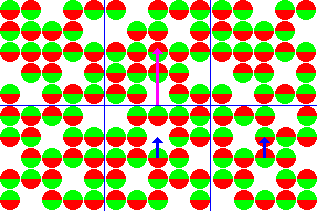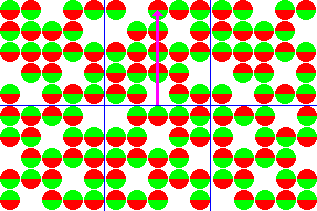
Для преобразования в общепринятую ЯМР систему координат, внешнее магнитное поле и вектор общей намагниченности направляются вдоль оси Z.

T1-процессы

В состоянии равновесия, вектор суммарной намагниченности параллелен направлению примененного магнитного поля Bo и называется равновесной намагниченностью Mo. В этом состоянии, Z-составляющая намагниченности MZ равна Mo. Еще MZ называется продольной намагниченностью. В данном случае, поперечной (MX или MY) намагниченности нет.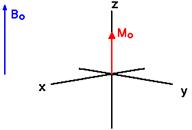

Суммарную намагниченность можно изменить, подвергнув ядерный спин воздействию энергией частоты равной разности энергии между спиновыми состояниями. Если в систему поступило достаточно энергии, можно насытить спиновую систему и сделать MZ=0.

Временная константа, описывающая, как MZ возвращается к равновесному значению, называется временем спин-решеточной релаксации (T1). Это явление описывается уравнением, являющимся функцией от времени t, которое после преобразования имеет вид:

Mz = Mo ( 1 - e-t/T1 )

поэтому T1 определяется как время, необходимое для того, чтобы изменить Z-составляющую намагниченности коэффициентом е.

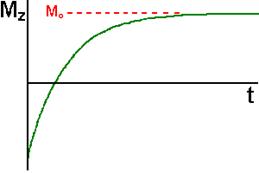Если суммарная намагниченность стала направлена вдоль отрицательного направления оси Z, она постепенно вернется в состояние своего равновесия вдоль положительного направления оси Z, со скоростью, определяемой T1. Это явление описывается уравнением, являющимся функцией от времени t, которое после преобразования имеет вид:

Mz = Mo ( 1 - 2e-t/T1 )

Время спин-решеточной релаксации (T1) - это время необходимое для уменьшения разности между продольной намагниченностью (MZ) и ее равновесным значением с коэффициентом е.

Если суммарная намагниченность расположена в плоскости XY , она будет вращаться вокруг оси Z с частотой, равной частоте фотона, который вызывает переход между двумя энергетическими уровнями спина. Эта частота называется частотой Лармора.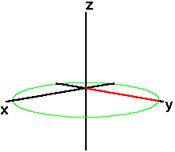

T2-процессы

В дополнение к вращению вектор суммарной намагниченности начинает сдвигаться по фазе (расфазировываться) из-за того, что каждый спиновый пакет испытывает магнитное поле, немного отличающееся от магнитного поля, испытываемого другими пакетами, и вращается со своей собственной частотой Лармора. Чем больше проходит времени, тем больше фазовая разница. В данном случае, вектор суммарной намагниченности изначально направлен вдоль положительного направления оси Y. Для этого примера и других примеров расфазировок представим себе этот вектор, как несколько более тонких перекрывающихся векторов от отдельных спиновых пакетов.

Временная константа, описывающая поведение поперечной намагниченности, MXY, называется спин-спиновым временем релаксации, T2.

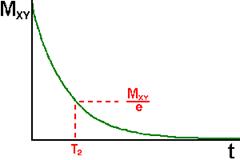
MXY =MXYo e-t/T2

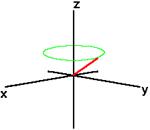T2 всегда меньше чем T1. Суммарная намагниченность в плоскости XY стремится к нулю, и затем продольная намагниченность возрастает до тех пор пока Mo не будет вдоль Z.

Любая поперечная намагниченность ведет себя таким же образом. Поперечный компонент вращается вокруг направления намагниченности и расфазировывается. Скорость возвращения продольной намагниченности определяется T1.

Подводя итоги, время спин-спиновой релаксации, T2, это время необходимое для уменьшения поперечной намагниченности с коэффициентом е. До этого, T2-и T1-процессы для простоты рассматривались отдельно. Например, перед возрастанием вдоль оси Z, вектора намагниченности полностью заполняли плоскость XY . В действительности же, оба процесса имеют место одновременно, лишь с тем ограничением, что T2 меньше или равно T1.

Два фактора приводящие к уменьшению поперечной намагниченности: 1) молекулярные взаимодействия (приводят к чистому T2 молекулярному эффекту) 2) изменения в Bo (приводят эффекту неоднородности T2). Сочетание этих факторов приводит к уменьшению поперечной намагниченности. Объединенная временная постоянная носит название T2 со звездочкой и обозначается символом T2*. Зависимость T2 от молекулярных процессов и от неоднородностей магнитного поля имеет следующий вид:

1/T2* = 1/T2 + 1/T2inhomo.

Вращающаяся система координат

Мы только что увидели поведение спинов в лабораторной системе координат. Удобнее было бы использовать вращающуюся систему координат, которая вращалась бы вокруг оси Z с частотой Лармора. Мы будем отличать эту систему координат от лабораторной системы по штрихам у обозначений осей X и Y, X'Y'.

Вектор намагниченности, вращающейся с частотой Лармора в лабораторной системе координат, окажется неподвижным, в системе, вращающейся вокруг оси Z. Во вращающейся системе релаксация намагниченности MZ в ее равновесное значение будет выглядеть также, как выглядело в лабораторной системе.

 Скачать реферат