Теоретические основы электротехники

I2=E2/R2=10/5=2A

Эквивалентная схема после замены источников ЭДС на источники тока:

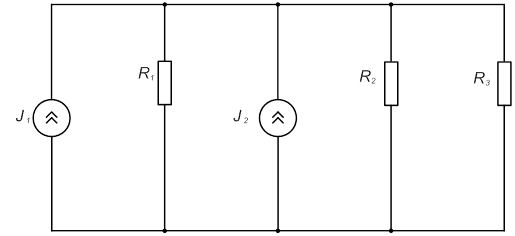
2) Так как

источники тока I1 и I2 включены параллельно, их можно заменить одним Iэкв.; параллельно включенные сопротивления R1 и R2 — сопротивлением Rэкв.

Iэкв.= I1 + I2 = 11+2=13A

1/Rэвк. = 1/R1 + 1/R2 = 1/2+1/5=7/10 Ом

Rэкв. = 10/7= 1,43Ом

Эквивалентная схема после замены нескольких источников тока одним:

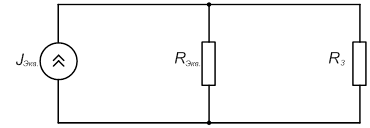
3) Источник тока Iэкв. и сопротивление Rэкв., включенное параллельно ему, преобразуется в источник ЭДС с внутренним сопротивлением Rэкв.

Eэкв. = Iэкв. ∙ Rэкв. =13×1,43 = 18,6 В

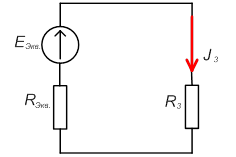
что приводит к схеме:

4) По закону Ома находим ток I3.

I3 = Eэкв./Rэкв.+R3 = 18,6/15+1,43 = 1,13А

Ответ: I3 =1,13A

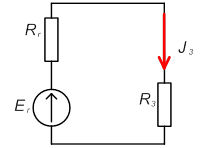
Метод эквивалентного генератора

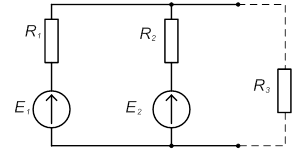
Определяем ЭДС Eг эквивалентного генератора одним из методов расчёта. Например, составив контурное уравнение по II закону Кирхгофа.

I1 (R1+R2) = E1-E2

найдём ток I1 = I2

I1=I2= (E1-E2) / (R1+R2)

I2= 12/7= 1,7A

Тогда: Ег = U12 = E2 + I 2R2

Eг = U12 = 10+1,7∙5 = 18,5A

2) Находим внутреннее сопротивление Rг эквивалентного генератора, с учётом того, что по отношению к его зажимам 1-2 сопротивления R1 R2 включены параллельно, т.е.

Rг=R1× R2/ (R1+R2)

Rг=2×5/ (2+5) =1,43Ом

3) По закону Ома находится ток I3

I3 =Eг/ (Rг+R3)

I3= 18,5/ (1,43+15) = 1,13A

Ответ: I3=1,13A

Метод узловых потенциалов.

Определяется напряжение U12 между узлами 1 и 2 по выражению:

U12 = (E1 G1 + E2 G2) / (G1 +G2 +G3)

G1=1/R1=1/2=0,5; G2= 1/R2 =1/5=0,2;

G3= 1/R3 =1/15=0,066

U12= (22×0,5 +10×0,2) / (0,5+0,2+0,066) = 16,97B

2) По закону Ома находится ток I3

I3 = U12/R3

I3= 16,97 /15 =1,13A

Ответ: I3 = 1,13A

Метод суперпозиции. Источник ЭДС Е2 заменяется его внутренним сопротивлением (в рассматриваемой задаче приняты идеальные источники ЭДС, то есть их внутренние сопротивления равны 0)

Схема для определения частичного тока, создаваемого источника ЭДС Е1:

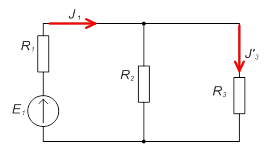
2) Находится частичный ток I3 c использованием правил определения эквивалентных сопротивлений при параллельном и последовательном соединении пассивных элементов и закона Ома.

а) эквивалентное сопротивление R23 параллельно включенных сопротивлений R1 и R2

R23 = R2×R3/ (R2+R3) = 5×15/ (5+15) = 3,75 Ом

Полное сопротивление цепи

Rц = R1+R23 = 2 +3,75 = 5,75 Ом

б) Ток II в неразветвленной части цепи:

II=E1/Rц = 22/5,75 = 3,82А

в) напряжение на сопротивлении R3

U3 = U23 =I1× R23 U3 = 3,82×3,75 = 14,34 B

г) частичный ток I3'

I3' = U3/R3 = 14,34/15 = 0,956 A

3) Для определения частичного тока I3'' расчет следует повторить, оставив в цепи только источник ЭДС Е2.

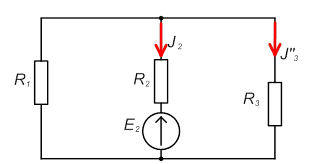
а) эквивалентное сопротивление R13 параллельно включенных сопротивлений R1 и R3

R13 = R1×R3/ (R1+R3) = 2×15\ (2+15) = 1,76 Ом

Полное сопротивление цепи

Rц = R2+R13 = 5 +1,76 = 6,76 Ом

б) Ток I2 в неразветвленной части цепи:

I2 = E2/Rц = 10/6,76 = 1,47A

в) напряжение на сопротивлении R3

U3 = U13= I 2×R13

U3 = 1,47×1,76 = 2,6B

г) частичный ток I3''

I3''= U3/R3 = 2,6/15 = 0,17A

4) Действительный ток I3

I3 = I3' + I3''

I3 = 0,956 + 0,17 = 1,13A

Ответ: I3 = 1,13А

Раздел 2

Для данной схемы состоящей из источников ЭДС и тока, активных, индуктивных и ёмкостных сопротивлений:

найти линейную частоту;

определить действующие значения токов во всех ветвях схемы и напряжения на всех комплексных сопротивлениях и каждом пассивном элементе;

определить полную, активную и реактивную мощности каждого источника электроэнергии и всех действующих в цепи источников;

составить баланс активных мощностей;

записать уравнения мгновенных значений ЭДС для источников ЭДС;

построить векторные диаграммы токов и напряжений

R1=10Ом; R2=40Ом; R4=25Ом; R5=15Ом;

L1=65мГн; L6=50мГн;

C1=65мкФ; C3=250мкФ; C4=125мкФ;

Еm2=24,5B ψ=80°; Еm6=24,5B ψ=-10°;

ω=400рад/с;

Jm5=5,5A ψ=0°

Решение:

Для определения линейной частоты f следует использовать связывающее её с угловой частотой ω соотношение

ω=2πf

f= ω/2π=400/2×3,14=63,69рад/с

Расчёт токов в ветвях следует вести в изложенной ниже последовательности

а) сопротивление реактивных элементов

XL= ω×L

XC=1/ ω×С

XL1= ω×L1=400×65×10-3=26Ом

XC1=1/ ω×С1=1/400×65×10-6=1/0,026=38,5Ом

XC3=1/ ω×С3=1/400×250×10-6=1/0,1=10Ом

XC4=1/ ω×С4=1/400×125×10-6=1/0,05=20Ом

XL6= ω×L6=400×50×10-3=20Ом

б) заданные числа в комплексной форме

Z1=R1+j (XL1 - XC1) =10+j (26-38,5) =10-j12,5=16e-j51°34'

À=a-jb=Aejφ

=arctg (-12,5/10) =-51°34'

A=

Z2=R2=40=40ej0°

Z3=-j XC3=-j10=10e-j90°

Z4= R4-j XC4=25-j20=32,015e-j36°66'

Z5= R5=15=15ej0°

Z6=j XL6=j20=20ej90°

в) преобразуем источник тока J5 в источник ЭДС E с внутренним сопротивлением Z5

E= J5Z5=5,5ej0°×15ej0°=82,5ej0°

Таблица 1-Результаты расчёта заданных величин и параметров схемы в алгебраической и показательной форме.

 Скачать реферат