Теоретические основы электротехники

Раздел 3

Трёхфазный приёмник электрической энергии соединён звездой и включен в четырёхпроводную сеть трёхфазного тока с линейным напряжением UЛ=660В. Сопротивления фаз приёмника: активные-RА=20Ом, RВ=16Ом, RС=16Ом; индуктивные-XLв=12Ом; ёмкостные-XCC=12Ом; сопротивления нулевого провода: активное-R0=0

,6Ом, индуктивное-X0=0,8Ом.

Определить:

1) Напряжение смещения нейтрали

а) при наличии нулевого провода;

б) при обрыве нулевого провода;

2) напряжение на каждой фазе приёмника

а) при наличии нулевого провода;

б) при обрыве нулевого провода;

3) при наличии нулевого провода

а) фазные, линейные токи и ток в нулевом проводе;

б) активную, реактивную и полную мощности каждой фазы и всей цепи;

в) коэффициент мощности каждой фазы и всей цепи.

Построить:

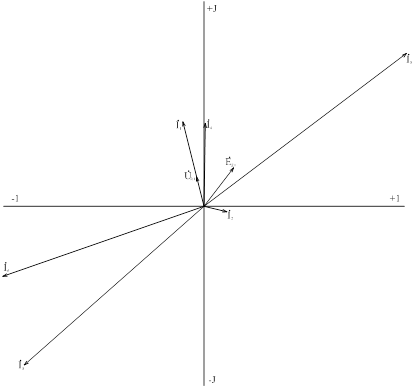
а) векторную диаграмму токов и напряжений для цепи с неповреждённым нулевым проводом;

б) векторную диаграмму токов и напряжений для цепи с оборванным нулевым проводом;

в) топографическую диаграмму напряжений при обрыве нулевого провода.

Решение: напряжение смещения нейтрали.

Напряжение смещения нейтрали U0 может быть найдено методом узловых потенциалов где ŮА, ŮB, ŮC,-фазные напряжения фаз А, В, и С; GA, GB, GC и G0 - проводимости фаз А, В, С и нулевого провода.

При соединении фаз звездой действующие значения фазных UФ. и линейных UЛ. напряжений связаны соотношением

UФ. = UЛ. /

Таким образом, ŮА=ŮB=ŮC=660/=380В.

Комплексы напряжений, сопротивлений и проводимостей в показательной и алгебраической формах:

ŮА=380ej0= (380+j0) В;

ŮB=380e-j120°= (-190-j328) В;

ŮC=380ej120°= (-190+j328) В;

ZA=20=20ej0°

GA=1/ ZA=1/20ej0°=0,05ej0°

ZB=16+j12=20ej37°

GB=1/ ZB=1/20ej37°=0,04-j0,03=0,05e-j37°

ZC=16-j12=20e-j37°

GC=1/ ZC=1/20e-j37°=0,04+j0,03=0,05ej37°

Z0=0,6+j0,8=1ej53°

G0=1/ Z0=1/1ej53°=0,6-j0,8=1e-j53°

Напряжение смещения нейтрали по:

Ů0= (ŮА×GA+ŮB×GB+ŮC×GC) / (GA+GB+GC+G0),

а) при наличии нулевого провода

Ů0= (380ej0×0,05ej0°+380e-j120°×0,05e-j37°+380ej120°×0,05ej37°) /

/0,05+ (0,04-j0,03) + (0,04+j0,03) + (0,6-j0,8) =-9,88-j10,83=14,66e-j132°38'

б) при обрыве нулевого провода

Ů'0= (380ej0×0,05ej0°+380e-j120°×0,05e-j37°+380ej120°×0,05ej37°) /

/0,05+ (0,04-j0,03) + (0,04+j0,03) =-122,15+j0=122,15ej180°

Определение фазных напряжений нагрузки

Напряжение на каждой фазе нагрузки Ůнагр. является разностью фазного напряжения источника питания Ů и напряжения смещения нейтрали Ů0

Ůнагр. = Ů - Ů0

Напряжение на фазах нагрузки

а) при наличии нулевого провода

ŮАнагр. =ŮА-Ů0=380- (-9,88-j10,83) =389,88+j10,83=390ej1°59'

ŮВнагр. =ŮВ-Ů0= (-190-j328) - (-9,88-j10,83) =-180,12-j317,17=364,74e-j120°

ŮCнагр. =ŮC-Ů0= (-190+j328) - (-9,88-j10,83) =-180,12+j338,83=383,73ej118°

б) при обрыве нулевого провода

Ů'Анагр. =ŮА-Ů'0=380- (-122,15+j0) =502,15+j0=502,15ej0°

Ů'Внагр. =ŮВ-Ů'0= (-190-j328) - (-122,15+j0) =-67,85-j328=334,94e-j102°

Ů'Cнагр. =ŮC-Ů'0= (-190+j328) - (-122,15+j0) =-67,85+j328=334,94ej102°

3) Определение фазных и линейных токов, тока в нулевом проводе

При соединении звездой фазные и линейные токи равны, т.е.

IФ. А=IЛ. А; IФ. В=IЛ. В; IФ. С=IЛ. С;

Если известны напряжения Ů и проводимости G-участков, токи через них можно определить по закону Ома

İ= Ů×G

а) Фазные и линейные токи при наличии нулевого провода

İф. А=İл. А=ŮАнагр. ×GA= (389,88+j10,83) ×0,05=19,494+j0,5415=19,50ej1°59'

İф. B=İл. B=ŮBнагр. ×GB= (-180,12-j317,17) × (0,04-j0,03) =-16,7190-j7,28=

=18,237e-j156°46'

İф. C=İл. C=ŮCнагр. ×GC= (-180,12+j338,83) × (0,04+j0,03) =

=-17,3697+j8,1496=19,1865ej155°

Ток в нулевом проводе

İ0=Ů0×G0= (-9,88-j10,83) × (0,6-j0,8) =-14,592+j1,406=14,659ej175°

Этот же ток может быть найден по второму закону Кирхгофа.

İ0= İф. А+ İф. B+ İф. C= (19,494+j0,5415) + (- 16,7190-j7,28) + (- 17,3697+j8,1496) =-14,592+1,406=14,659ej175°

б) Фазные и линейные токи при обрыве нулевого провода

İ'ф. А=İ'л. А=Ů'Анагр. ×GA= (502,15+j0) ×0,05=25,1075=25,1075ej0°

İ'ф. B=İ'л. B=Ů'Bнагр. ×GB= (-67,85-j328) × (0,04-j0,03) =-12,554-j11,0845=

=16,747e-j138°55'

İ'ф. C=İ'л. C=Ů'Cнагр. ×GC= (-67,85+j328) × (0,04+j0,03) =-12,554+j11,0845=

=16,747ej138°55'

Ток в нулевом проводе

İ'0=Ů'0×G0 т.к при обрыве нулевого провода его проводимость равна 0

4а) Определение мощностей

Полные мощности фаз SФ находятся как произведение комплексов фазных напряжений ŮФ на сопряжённые комплексы фазных токов İф SФ= ŮФ× İф Полная мощность каждой фазы

SА= ŮАнагр. ×İф. А= (389,88+j10,83) × (19,494-j0,5415) =7606,185+j0=7606,185ej0°

SB= ŮBнагр. ×İф. B= (-180,12-j317,17) × (-16,7190+j7,28) =5320,585+j3991,777=6651,535ej36°88'

SC= ŮCнагр. ×İф. C= (-180,12+j338,83) × (-17,3697-j8,1496) =5889,959-j4417,469=7362,449e-j36°88'

Полная мощность всей нагрузки

S=SА+SB+SC= (7606,185+j0) + (5320,585+j3991,777) + (5889,959-j4417,469) =18816,729-j425,695=18821,543e-j1°29'

Активная и реактивная мощности фаз и всей нагрузки находятся как действительная и мнимая части соответствующих комплексов полных мощностей т.е. активная мощность фаз

PA=7606,185Вт

PB=5320,585 Вт

PC=5889,959 Вт

активная мощность всей нагрузки

P=18816,729Вт

реактивная мощность фаз

QA=0

QB=3991,777ВАр

QC=-4417,469ВАр

реактивная мощность всей нагрузки

Q=-425,695ВАр

Активная мощность каждой фазы может быть найдена по выражению

PA=ݲф. А×RфА=19,50²×20=7606Вт

PВ=ݲф. В×RфВ=18,237²×16=5321Вт

PС=ݲф. С×RфС=19,1865²×16=5889,9Вт

4б) Определение коэффициентов мощности

Коэффициент мощности cosφ является отношением действительных частей комплексов полной мощности или полного сопротивления к их модулям

сosφ=a/A,

где a-действительная часть комплекса

А - модуль величины

Таким образом коэффициенты мощности фаз, найденные с использованием различных величин, при правильном решении должны совпасть.

 Скачать реферат