Расчет профиля диффузии сурьмы в кремнии
Диффузия сурьмы будет идти практически стопроцентно по вакансионному механизму [1], так как сурьма – элемент пятой группы и относительный вклад междоузельного механизма составляет порядка 1%. Коэффициент диффузии будем рассчитывать по уравнению (44).
Сурьма – донорная примесь, она будет диффундировать только по нейтральным и отрицательно заряженным вакансиям. Кроме того, двукратно отрицател
ьно заряженные дефекты в силу их незначительного влияния можно не учитывать.
Таким образом, выражение для коэффициента диффузии примет вид:
![]() (45)
(45)
Согласно уравнению Аррениуса:
 (46)
(46)
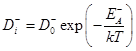 , (47)
, (47)
Т.о. 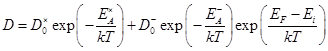 (48)
(48)
Аррениусовские параметры приведены в табл. 1 [1]:
Таблица 1. Аррениусовские параметры Sb в Si[3]
|
Примесь |
Sb |
|
|
0,214 |
|
|
3,65 |
|
|
15,0 |
|
|
4,08 |
То есть для определения коэффициента диффузии необходимо знать зависимость положения уровня Ферми от температуры. Для его определения воспользуемся уравнением электронейтральности:
![]() (49)
(49)
В данном уравнении вкладом слагаемого ![]() можно пренебречь.
можно пренебречь.
Введем обозначение ![]() .
.
Концентрации электронов и дырок можно выразить через концентрацию собственных носителей.
![]() (50)
(50)
![]() (51)
(51)
Концентрации заряженных дефектов также являются функциями температуры:
![]()
![]() (52)
(52)
![]()
![]() (53)
(53)
![]()
![]() (54)
(54)
![]()
![]() (55)
(55)
Аналогично находим:
 (56)
(56)
 (57)
(57)
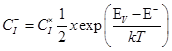 .(58)
.(58)
Поскольку акцепторные энергетические уровни заряженных дефектов жёстко привязаны к дну зоны проводимости ![]() , а донорные - к потолку валентной зоны
, а донорные - к потолку валентной зоны ![]() , то справедливы следующие положения энергетических уровней [1]:
, то справедливы следующие положения энергетических уровней [1]:![]()
![]() (59)
(59)
![]()
![]()
Совершенно аналогично для междоузельных атомов:
![]()
![]() (60)
(60)
![]()
Также находим ![]() :
:
![]() (61)
(61)
![]() (62)
(62)
![]() (63)
(63)
![]() (64)
(64)
Подставляя эти величины в выражения для концентрации заряженных дефектов, а их, в свою очередь в уравнение электронейтральности, получаем уравнение вида:
![]() (65)
(65)
Из него мы определяем х.
Коэффициенты А, В, С и P имеют вид:
![]() (66)
(66)
![]() (67)
(67)
![]() (68)
(68)
![]() , где(69)
, где(69)
![]() , (70)
, (70)
 , (71)
, (71)
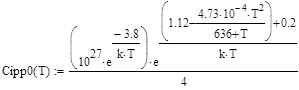 , (72)
, (72)
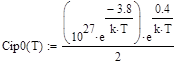 , (73)
, (73)
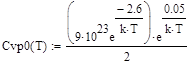 , (74)
, (74)
 , (75)
, (75)
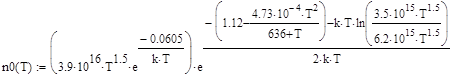 , (76)
, (76)
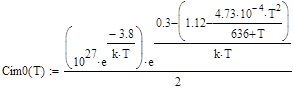 , (77)
, (77)
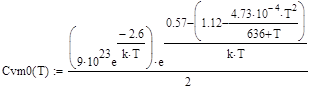 , (78)
, (78)
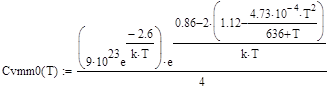 . (79)
. (79)
В эти выражения входят равновесные концентрации вакансий и междоузлий, которые можно определить из (25).
Температурную зависимость для ширины запрещенной зоны определяет соотношение Варшни:
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода
