Механические колебания

Как видно, амплитуда Aрезрезультирующего колебания зависит от разности фаз складываемых колебаний.

Рассмотрим два крайних случая:

А) Колебания происходят в фазе, то есть a01 = a02, тогда и , поэтому Aрез = 2A.

Если амплитуды не равны, A

рез = A1 + A2.

Б) Колебания происходят в противофазе, то есть a01 = a02 ± p, тогда . Следовательно, и Aрез = 0. Если амплитуды не равны, например, A1 > A2, тоAрез = A1 - A2.

Таким образом, при сложении двух одинаково направленных гармонических колебаний одного периода и с равными амплитудами получается гармоническое колебание того же периода с амплитудой, которая в зависимости от соотношения фаз складываемых колебаний может изменяться от удвоенного значения, если колебания происходят в фазе, до нуля, если они находятся в противофазе.

При сложении гармонических колебаний с разными частотами результирующее колебание не будет гармоническим, а будет являться сложным колебанием (Рис.4.).

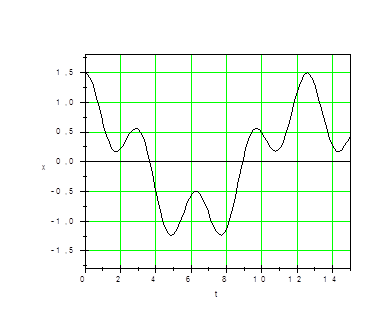
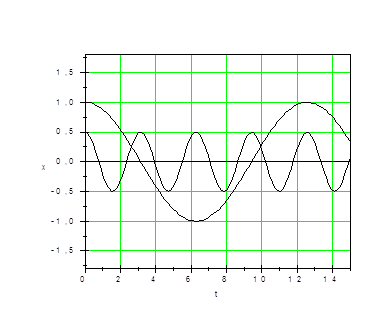
Рис. 4. Сложение гармонических колебаний с разными частотами:

А) исходные колебания, Б) результирующее колебание.

Сложное колебание и его гармонический спектр.

Согласно теореме Фурье, любое сложное колебание может быть представлено как сумма простых (гармонических) колебаний (гармоник), периоды или частоты которых кратны основному периоду или частоте сложного колебания.

Совокупность простых колебаний, на которые можно разложить данное сложное колебание, называется его гармоническим спектром.

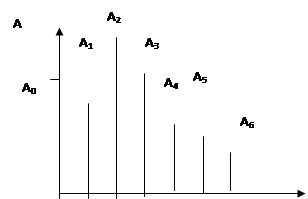
В гармоническом спектре сложного колебания указываются частоты и амплитуды всех составляющих его простых колебаний. Обычно спектр изображается в виде графика, на горизонтальной оси которого откладываются частоты; затем для каждой из частот простых колебаний имеющихся в спектре, строится ордината, соответствующая амплитуде этого колебания. Если гармонический спектр сложного колебания содержит только небольшое число простых колебаний и график его состоит из отдельных ординат, то такой спектр называется линейчатым (рис. 5.).

Если спектр содержит простые колебания практически всех частот в каких-то пределах, то он называется сплошным и график его строится в виде сплошной огибающей кривой.

Установление гармонического спектра является основным приемом при анализе сложного колебания. Этот анализ делается с помощью специальных приборов —гармонических анализаторов. Они применяются и в медицине при исследовании, например, колебаний биопотенциалов головного мозга и др. Многие процессы человеческого организма являются периодическими: сердечные сокращения, дыхание, кровенаполнение сосудов и т. п

				w

Сложение взаимно-перпендикулярных колебаний.

В результате сложения двух взаимно-перпендикулярных колебаний различного периода тело движется по сложным фигурам, форма которых зависит от соотношения периодов, амплитуд и начальных фаз складываемых колебаний и которые называются фигурами Лиссажу.

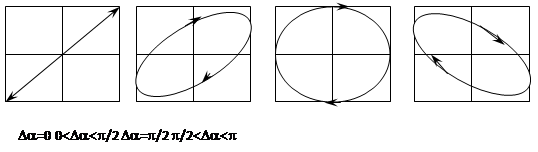
Рис. 6. Фигуры Лиссажу для колебаний различающихся начальными фазами Da.

1.4 Механические волны, их виды и скорость распространения

Колебательная система может отдавать энергию во внутреннюю среду. Эта передача энергии становится возможной благодаря тому, что частицы среды сами представляют собой миниатюрные колебательные системы. Молекулы среды связаны друг с другом силами, законы которых в известных границах подобны законам упругих сил. Если одна из частиц окажется выведенной из положения равновесия, то силы, действующие на нее со стороны соседних частиц, заставляют ее вновь вернуться к устойчивому положению. Вместе с тем, по закону равенства действия и противодействия, соседние частицы также подвергнутся влиянию смещающих сил и в свою очередь будут выведены из устойчивого положения. Таким образом, каждое возмущение, однажды возникнув в определенном участке среды, будет постепенно распространяться, захватывая частицы, все дальше и дальше отстоящие от места начального возмущения.

Колебательный процесс благодаря взаимодействию частиц будет распространяться в среде с некоторой конечной скоростью. Процесс распространения колебаний в среде называется волновым движением или просто волной. Для нашего случая это будет упругая или механическая волна.

Различают продольные и поперечные волны. Вид волн, распространяющихся в среде, существенно зависит от упругих свойств среды.

Волна, распространяющаяся в том же направлении, в котором происходят колебания частиц среды, называется продольной волной.

Продольные волны образуются в телах, обладающих упругостью объема, т.е. противодействующих деформации объемного сжатия. Это свойственно всем телам, поэтому они образуются в любых средах: твердых, жидких, газообразных. К продольным волнам, в частности, относятся звуковые, инфразвуковые и ультразвуковые.

Волна, в которой колебательное движение совершается перпендикулярно к направлению распространения колебаний, называется поперечной.

Поперечные упругие волны образуются только в твердых телах, которые обладают упругостью формы, т.е. противодействуют деформации сдвига (например, сейсмические волны в земной коре при землетрясениях; волны, бегущие вдоль натянутой струны; крутильные волны, вызываемые попеременным закручиванием и раскручиванием конца длинного стержня).

 Скачать реферат