Механические колебания

Рефераты / Физика и энергетика / Механические колебания

Содержание

1. Механические колебания

1.1 Механические колебания: гармонические, затухающие и вынужденные колебания

1.2 Автоколебания

1.3 Разложение колебаний в гармонический спектр. Применение гармонического анализа для обработки диагностических данных

1.4 Механические волны, их виды и скорость распространения

1.5 Энергетические характеристики волны

Список и

спользованных источников

1. Механические колебания

1.1 Механические колебания: гармонические, затухающие и вынужденные колебания

Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости (качание маятника часов, колебания струны или ножек камертона, напряжение между обкладками конденсатора в контуре радиоприемника, работа сердца).

В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические и т.д. Мы будем рассматривать механические колебания. Колебания, происходящие при отсутствии трения и внешних сил, называются собственными; их частота зависит только от свойств системы.

Простейшими являются гармонические колебания, т.е. такие колебания, при которых колеблющаяся величина (например, отклонение маятника) изменяется со временем по закону синуса или косинуса.

Дифференциальное уравнение гармонического колебания

Рассмотрим простейшую колебательную систему: шарик массой m подвешен на пружине.

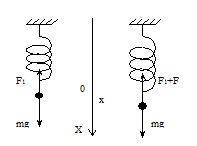
В этом случае упругая сила F1 уравновешивает силу тяжести mg. Если сместить шарик на расстояние х, то на него будет действовать большая упругая сила (F1 + F). Изменение упругой силы по закону Гука пропорционально изменению длины пружины или смещению шарика х:

F=-kx,(1)

где k — жесткость пружины. Знак "-" отражает то обстоятельство, что смещение и сила имеют противоположные направления.

Рис. 1

Сила F обладает следующими свойствами: 1) она пропорциональна смещению шарика из положения равновесия; 2) она всегда направлена к положению равновесия.

В нашем примере сила по своей природе упругая. Может случиться, что сила иного происхождения обнаруживает такую же закономерность, то есть оказывается равной - kx. Силы такого вида, неупругие по природе, но аналогичные по свойствам силам, возникающим при малых деформациях упругих тел, называют квазиупругими.

Уравнение второго закона Ньютона для шарика имеет вид:

, или .

Так как k и m — обе величины положительные, то их отношение можно приравнять квадрату некоторой величины w0, т.е. мы можем ввести обозначение . Тогда получим

Підпис:

(2)

Таким образом, движение шарика под действием силы вида (1) описывается линейным однородным дифференциальным уравнением второго порядка.

Легко убедиться подстановкой, что решение уравнения имеет вид:

(3)

где (w0 t + a0) = a — фаза колебаний; a0 — начальная фаза при t = 0; w0 — круговая частота колебаний; A — их амплитуда.

Итак, смещение x изменяется со временем по закону косинуса.

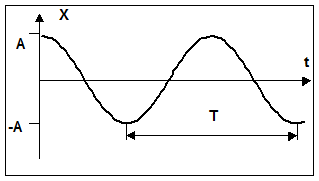
Следовательно, движение системы, находящейся под действием силы вида f = - kx, представляет собой гармоническое колебание. График гармонического колебания показан на рисунке. Период этих колебаний находится из формулы:

Для пружинного маятника получаем:

Круговая частота связана с обычной n соотношением: .

Энергия при гармоническом колебании

Выясним, как изменяется со временем кинетическая Еk и потенциальная Еп энергия гармонического колебания. Кинетическая энергия равна:

, (4)

где k = m w02.

Потенциальную энергию находим из формулы потенциальной энергии для упругой деформации и используя (3):

EП. (5)

Складывая (4) и (5), с учетом соотношения , получим:

E = EK + EП = . (6)

Таким образом, полная энергия гармонического колебания остается постоянной в отсутствие сил трения, во время колебательного процесса кинетическая энергия переходит в потенциальную и наоборот.

Затухающие колебания

Колебания, происходящие в системе при отсутствии внешних сил (но при наличии потерь на трение или излучение), называются свободными. Частота свободных колебаний зависит от свойств системы и интенсивности потерь.

Наличие трения приводит к затухающим колебаниям. Колебания с убывающей амплитудой называются затухающими.

Допустим, что на систему, кроме квазиупругой силы, действуют силы сопротивления среды (трения), тогда второй закон Ньютона имеет вид:

. (7)

Ограничимся рассмотрением малых колебаний, тогда и скорость системы будет малой, а при небольших скоростях сила сопротивления пропорциональна величине скорости:

, (8)