Комплексная статистическая обработка экспериментальных данных

Анализируя полученные данные, можно сделать вывод о том что значения медианы и среднего арифметического для выборок случайной величины и имеют практически равное значение. Для выборки значение коэффиц

иента ассиметрии, а для выборки случайной величины значение эксцесса практически равно 0. Для случайной величины значение эксцесса практически -1,2. Таким образом, все это свидетельствует о близости распределения случайной величины нормальному распределению, а случайной величины равномерному.

2.9 Определение закона распределения случайных величин

2.9.1 Определение закона распределения случайной величины по виду гистограммы

По виду гистограмм, приведенных на рисунках 2.19-2.21 делаем предположение о том, что случайная величина подчиняется равномерному закону распределения, а случайная величина соответствует нормальному закону распределения, что можно увидеть на рисунках 2.22-2.24.

2.9.2 Определение оценок параметров распределений

Метод моментов

Метод моментов заключается в том, что определенное количество статистических начальных и (или) центральных моментов приравнивается к соответствующим теоретическим моментам распределения случайной величины. Уравнения метода показано в формуле (2.23).

.

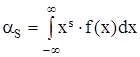– статистическая оценка соответствующего теоретического момента -того порядка, вычисляется по формуле (2.25):

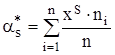– теоретический центральный момент s-того порядка, вычисляется по формуле (2.26):

– статистическая оценка теоретического центрального момента -того порядка, вычисляется по формуле (2.27):

Из системы (2.23) находятся параметры распределения. Число уравнений в системе зависит от количества неизвестных параметров. Для нормального и равномерного законов, система должна содержать два уравнения, для экспоненциального – одно.

Для равномерного закона распределения система (2.23) принимает вид (2.28):

Из системы 2.28 нужно найти параметры и .

В таблице 2.38 приведены значения этих параметров, найденные методом моментов и методом максимального правдоподобия.

Таблица 2.38 – Значения параметров и

 Скачать реферат