Анализ систем автоматического управления

где

Строим графики логарифмических характеристик разомкнутой системы, с помощью MATLAB (оператор bode или margin) Рис. 1.3 а.

Рис. 1.3а

Строим график АФЧХ с помощью MATLAB (оператор nyquist) рис. 1.3 б для разомкнутой системы.

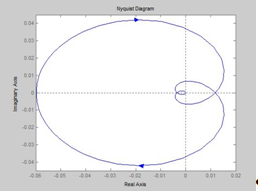
Рис 1.3 б

Запасы устойчивости по модулю и фазе определяются по логарифмическим характеристикам (см. рис. 1.3 а): на частоте среза wс определяется запас по фазе —∆φ, а запас по амплитуде ∆L - на частоте при которой φ(w) = -180. Таким образом, ∆L≈0. 1дБ, ∆φ≈ 0°, что является недостаточным.

4. Величина ошибки по скорости определяется как eск=V1/K. Для ориентировочной оценки tпп и σ следует построить переходной процесс h(t) (оператор step в MATLAB) при v(t) = 1[t] и по нему определить tпп и σ.

Для получения уравнений состояний в нормальной форме используем дифференциальное уравнение замкнутой системы

D(s)y(t)=Kv(t). Если D(s)=b0s4+b1s3+b2s2+b3s+b4=0, ,то уравнение состояния имеет вид

Для описания динамических систем в пространстве состояний в Matlab применяются модели подкласса ss, которые основаны на линейных дифференциальных или разностных уравнениях.

Модель непрерывной системы в подклассе ss имеет вид:

где: х - вектор состояния; v- вектор входа; у - вектор выхода.

Для формирования моделей в подклассе ss предназначена функция ss

sys=ss(A,B,C,D)

В результате под именем sys получаем ss-объект с числовыми характеристиками в виде четверки матриц {А, В, С, D}, которые должны иметь согласованные размеры. Матрицу D в данном случае полагаем равной 0.

Для построения переходного процесса h(t) воспользуемся оператором step в MATLAB.

Реализация функций имеет вид:

sys=ss([0 1 0 0;0 0 1 0;0 0 0 1;-b4/b0 -b3/b0 -b2/b0 -b1/b0],[0 0 0 K/b0]', eye(4), zeros(4,1))

a =

x1 x2 x3 x4

x1 0 1 0 0

x2 0 0 1 0

x3 0 0 0 1

x4 -104.6 -32.26 -168.5 -36.16

b =

u1

x1 0

x2 0

x3 0

x4 104.6

c =

x1 x2 x3 x4

y1 1 0 0 0

y2 0 1 0 0

y3 0 0 1 0

y4 0 0 0 1

d =

u1

y1 0

y2 0

y3 0

y4 0

Continuous-time model.

>> step(sys)

В результате получим графики представленные на рис. 1.4. Нас будетинтересовать Out(l). Величина ошибки по скорости определяется как:

еск=V1/K = 1,4/3,243 = 0,432>ескзад = 0,04.

Для ориентировочной оценки tnn и о следует построить переходной процесс h{t) (оператор step в MATLAB) при v(t)=1(t) и по нему определить tпп и σ. Эти величины из графика Out(l) определяются следующим образом:

Время переходного процесса определяется с учетом следующих соотношений: εуст=v(t)/(l+K), где v(t)=l[t], а К=3,243 - общий коэффициент передачи разомкнутой системы. Тогда еуст= 1/(1+3,243)=0,236 и следовательно tпп из графика Out(l) tпп ≈50с > tппзад = 2.5с.

Рис 1.4

Таким образом, исходная система не удовлетворяет заданным показателям качества, ее следует скорректировать.

5. Если исходная система не удовлетворяет заданным показателям качества, ее следует скорректировать. В случае применения частотных методов синтеза коррекции строится желаемая ЛАЧХ Lж(w). В низкочастотной части желаемой ЛАЧХ при сохранении порядка астатизма (наличие интегратора 1/s в системе) требуемый коэффициент усиления выбирается из соотношения Kz=v1/eск=1,4 / 0.04 = 35. На частоте среза желательно иметь наклон ЛАЧХ -20 дБ/дек с протяженностью этого участка не менее одной декады. Далее среднечастотная часть ЛАЧХ сопрягается с низкочастотной отрезком прямой с наклоном -40(если необходимо -60) дБ/дек, а высокочастотная часть желаемой и исходной ЛАЧХ по возможности должны совпадать.

Учет требований качества переходного процесса: tпп и σ, запасов устойчивости учитываются при формировании среднечастотной области Lж(w). Здесь можно воспользоваться графиком (рис. 1.5).

Рис 1.5

По графику рис. 1.5 для заданных значений у и tnn находим wп, и затем из соотношения wc = (0.6 - 0.9) wп, частоту среза wc.

В наше случае: (как показано на рис.1.5) для у =10%, tр=3π/ωп ,откуда для tр значение ωп= 3π/1,5=6,8 1/с и ωc=5 1/с.

Сопряжение среднечастотного участка с низкочастотным и высокочастотным (рис. 1.6) должно быть таким, чтобы была проще коррекция и чтобы изломы, по возможности, были не более чем на 20 дБ/дек (протяженность участка около декады). Тогда, выберем L2≈10дБ на частоте ω2=(0.1-0.5)ωс=2.5<ωс=5 и L3≈ -10 дБ на частоте ω3=25 ≥ ωс=5. Введем обозначения:

Величину ω1 найдем из условия равенства значений Lж(ω1)=Lисх(ω1). Это

соотношение приводит к следующему выражению:

В последнем выражении обозначено:

ω’=0.1w2

L’(ω’)=50 дБ

L’(ω2)=10 дБ

L(ω3p)=L(0.476)=21,18 дБ

L(ω2)=L(1.2)=-35,743 дБ

Последние две величины находятся из выражения для Lисх(w).

Найденное по формуле значение ω1=0.098

ЛАЧХ корректирующего устройства с характеристикой Lk(w) соответствует функция:

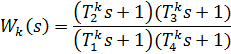
где:

Общая передаточная функция разомкнутой системы с корректирующим звеном последовательного типа имеет вид:

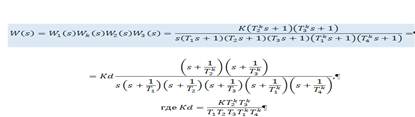
Далее воспользуемся функцией zpk(z, р, К), где z и р - векторы из нулей и полюсов, a Kd - обобщенный коэффициент передачи, sys - любое имя присваиваемое модели. Тогда запись в системе Matlab примет вид:

sys1=zpk([-1/t2k -1/t3k],[0 -1/t1 -1/t2 -1/t3 -1/t1k -1/t4k],kd)

Zero/pole/gain:

58.2 (s+2.5) (s+0.4762)

-------------------------------------------------

s (s+7.143) (s+4.167) (s+25) (s+0.4762) (s+0.097)

 Скачать реферат