Анализ систем автоматического управления

1.Исследование линейной непрерывной системы автоматического управления

Задание:

1) Найти передаточную функцию разомкнутой системы W(s) и передаточную функцию замкнутой системы Ф(s), ;

2) Построить область устойчивости системы в плоскости общего коэффициента передачи К = К1К2К3 и постоянной времени Т2 при задан

ных значения Т1 и Т3. Найти граничное значение при заданном значении Т2, при котором система выходит на границу устойчивости.

3) Построить графики логарифмических амплитудной и фазовой частотных характеристик L(w) и φ(w) при значении коэффициента передачи K=0,7K’.

4) Оценить запасы устойчивости по модулю ∆L и фазе ∆ φ, величину ошибки по скорости еск при v(t) = v1t и f= 0, время переходного процесса tp и перерегулирование σ в исходной системе при K=0,7K’.

5) Если исходная система не удовлетворяет заданным в таблице 1 показателям качества tp, σ, еск (хотя бы одному из них) или имеет малые запасы устойчивости, то провести коррекцию системы (последовательного или параллельного типа) и найти передаточную функцию корректирующего устройства.

6) Вычислить в скорректированной системе переходный процесс на выходе y(t) при подаче на вход единичной ступенчатой функции v(t)=1(t)( f= 0). Найти tp, σ по переходному процессу и сравнить их с требуемым по заданию.

Исходные данные:

Структура исследуемой замкнутой линейной непрерывной САУ представлена на рис. 1.1, где v(t)- управляющее воздействие, (f)- возмущающее воздействие, е(t)- сигнал ошибки, y(t)- выходной сигнал. Значения параметров Т1 Т2, Т3 заданы в табл. 1. Размерность Т1 Т2, Т3 в секундах, общий коэффициент передачи К = К1К2К3 имеет размерность 1/с, в табл. 1 заданы также желаемые показатели качества системы: максимальная ошибка по скорости еск при скачке по скорости v(t) = v1t и f= 0, время переходного процесса tп.п в секундах, и перерегулирование у в процентах.

Таблица 1. Структура исследуемой замкнутой линейной непрерывной САУ

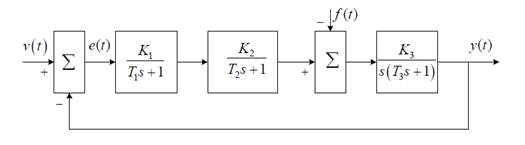
Рисунок 1.1

Выполнение:

1. Требуемые передаточные функции находят с использованием правил структурных преобразований. Коротко сформулируем основные правила:

— Передаточные функции последовательно соединенных звеньев перемножаются.

— Передаточные функции параллельно соединенных звеньев складываются.

Передаточная функция системы с обратной связью - это передаточная функция замкнутой системы, которая определяется по формуле:

(по условию)

Передаточная функция разомкнутой системы W(s) = Y(s)/U(s) при f= 0, e = u (т.е. разомкнута главная обратная связь) определится выражением:

где обозначим К = К1К2К3,

0,03135

1,12127

5,223

Главная передаточная функция или передаточная функция замкнутой системы при f = 0:

Передаточная функция по ошибке при f= 0, которая позволяет выразить ошибку e(t) в системе при известном входном воздействии:

Передаточная функция по возмущению при и = 0 позволяет выразить влияние возмущения на выходной сигнал:

2. . Передаточная функция разомкнутой исходной системы имеет вид W(s) = K/sL(s), где L(s) = (T1s+1)(T2s +1)(T3s+1). Характеристическое уравнение замкнутой системы будет D(s) = K+L(s)s = b0s4 +b}s3 +b2s2 +b3s + b4 =0, где при заданных из таблицы исходных данных числовых значениях Т1 и Т3 коэффициенты bj будут зависеть от параметров К и Т2. Применение критерия Гурвица к характеристическому уравнению четвертого порядка дает следующие условия устойчивости:

b3(b1b2-b0b3)-b4b12 > 0, b, > 0, i = 0, .,4.

Приравнивая в написанных соотношениях правые части нулю, найдем зависимость К от Т2 и построим в плоскости К и Т2 границы устойчивости, ограничивающие некоторую область устойчивости. При заданном параметре Т2 находим граничное значение КГР коэффициента передачи К.

К = К1К2К3

b0==0,165=с0

5,033с0

b3=1 b4=K

Выразим К через параметр Т2:

Зависимость К(Т2) приведена на рис. 1.2

Рис.1.2

Kгр=KT2=0.19=4,633

3. Полагая К = 0.7КГР, записываем аналитическое выражение для φ(w)= argW(jw), L(w) = 20lg|W(jw)| из W(s) при s = jw.

К=0.7Кгр= 3,243

Передаточную функцию разомкнутой системы можно записать в виде:

где

тогда:

 Скачать реферат