Некоторые интерполяционные свойства конечномерных сетевых пространств и пространств Лоренца
Эта теорема, напоминает теорему Рисса-Торина, но отличается от нее во многих важных отношениях.
Во-первых, здесь скаляры могут быть как вещественными, так и комплексными, в то время как в теореме Рисса-Торина обязательно нужно, чтобы скаляры были комплексными. Во-вторых здесь имеется ограничение p≤q. Наиболее важная особенность состоит в том, что в предпосылках теоремы пространства Таким образом, теорема Марцинкевича может оказаться применимой в тех случаях, где теорема Рисса-Торина уже не работает.
2. Общие свойства интерполяционных пространств
Пусть A - векторное пространство над полем вещественных или комплексных чисел. Оно называется нормированным векторных пространством, если существует вещественнозначная функция (норма) 1) 2) 3) Пусть A и B – два нормированных векторных пространства. Отображение T из A в B называется ограниченным линейным оператором, если
Ясно, что всякий ограниченный линейный оператор непрерывен.
Пусть A0 и A1 – топологических векторных пространства. Говорят, что
A0 и A1 совместимы, если существует отделимое топологическое векторное пространство U, такое, что A0 и A1, являются подпространствами. В этом случае можно образовать сумму A0 + A1, и пересечение A0∩A1. Сумма состоит из всех a Справедлива следующая лемма
Лемма 2.1. Пусть A0 и A1-совместимые нормированные векторные пространства. Тогда
A0∩A1, есть нормированное векторное пространство с нормой
A0 + A1, также представляет собой нормированное векторное пространство с нормой
При этом если A0 и A1 – полные пространства, то A0∩A1 и A0 + A1 также полны.
Дадим некоторые важные определения:
Категория σ состоит из объектов A,B,C…., и морфизмов R,S,T,…. между объектами и морфизмами определено трехместное отношение T: A↷B.
Если T: A↷B и S: B↷C, то существует морфизм ST, называемый произведением (или композицией) морфизмов S и T, такой, что ST: A↷ C.
Операция взятия произведения морфизмов удовлетворяет закону ассоциативности: T(SR)=(TS)R. далее, для всякого объекта A из σ существует морфизм I=IA, такой, что для любого морфизма T: A↷A TI=IT=T
Через σ1 обозначим категорию всех совместимых пар Определение 2.1. Пусть Если, кроме, того T: Более общим образом, пусть Если выполнено
В этом случае, говорят, что A и B равномерные интерполяционные пространства.
Определение 2.2 Интерполяционные пространства A и B называются пространствами типа θ (0≤θ≤1), если
В случае с=1 говорят, что A и B - точные интерполяционные пространства типа θ.
3. О норме и спектральном радиусе неотрицательных матриц
Хорошо известно, что проблема нахождения нормы линейного оператора, спектрального радиуса оператора являются трудной проблемой и в конечномерном случае. В то же время, иногда важно не вычисляя нормы оператора знать, как она изменится в случае некоторого преобразования.
В данной работе изучается влияние распределения ненулевых элементов неотрицательной матрицы на норму соответствующего оператора и спектрального радиуса.
Определим пространство a=(a1, a2,…, aN)
с нормой
Множество Q={(k,l):k,l=1,…,N} назовем решеткой размерности N x N. Любое множество Q0={(ki,lj): Спектральный радиус линейного оператора в конечномерном пространстве r(A)= где lk- собственные значения оператора A.
Пусть m ≤ N, d1,…,dm - положительные числа. Через Dm обозначим множество неотрицательных матриц А, ненулевые элементы которых принимают значения d1,…,dm. Через P(A) обозначим множество индексов соответствующих положительным элементам. Пусть AÎDm. Если D={(ki,lj), i=1,…,q, j=1,…,p} подрешетка, содержащая P(A), то для соответствующего оператора А
![]() заменены на более широкие пространства
заменены на более широкие пространства ![]() и
и ![]() .
.
![]() , определенная на A, удовлетворяющая условием.
, определенная на A, удовлетворяющая условием.
![]() , причем
, причем ![]()
![]() (λ-скаляр)
(λ-скаляр)
![]() .
.
![]() ,
, ![]() и
и  .
.
![]() U, представимых в виде a=a0+a1, где a0
U, представимых в виде a=a0+a1, где a0![]() A, и a1
A, и a1![]() A,
A,
![]()
![]()
![]() пространств из σ.
пространств из σ.
![]() =(A0,A1)-заданная пара из σ1. Пространство A из σ будем называть промежуточным между A0 и A1 (или относительно
=(A0,A1)-заданная пара из σ1. Пространство A из σ будем называть промежуточным между A0 и A1 (или относительно ![]() ), если имеют место непрерывные вложения.
), если имеют место непрерывные вложения.
![]() .
.
![]() ↷
↷ ![]() влечет T: A ↷ A, то A называется интерполяционным пространством между A0 и A1.
влечет T: A ↷ A, то A называется интерполяционным пространством между A0 и A1.
![]() и
и ![]() - две пары из σ1. Тогда два пространства A и B из σ называются интерполяционными относительно
- две пары из σ1. Тогда два пространства A и B из σ называются интерполяционными относительно ![]() и
и ![]() соответственно и T:
соответственно и T: ![]() ↷
↷ ![]() влечет T: A↷ B.
влечет T: A↷ B.
![]() ,
,
![]()
![]() как множество всех наборов вида
как множество всех наборов вида
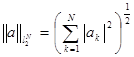 .
.
![]() ,
, ![]() } будет являться подрешеткой размерности r x m.
} будет являться подрешеткой размерности r x m.
![]() определяется следующим образом:
определяется следующим образом:
![]() ,
,
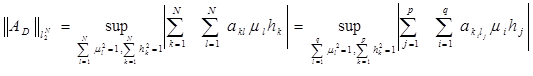
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
