Некоторые интерполяционные свойства конечномерных сетевых пространств и пространств Лоренца

.

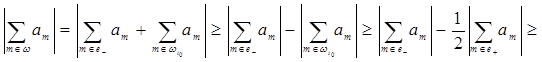
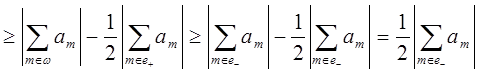Таким образом, получаем

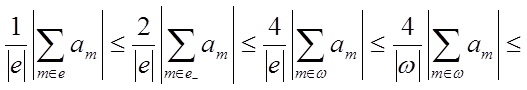
Из того, что

И

меем

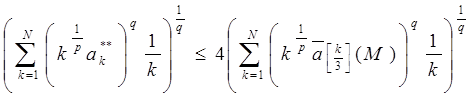
То есть . Следовательно ↪ где соответствующие константы не зависят от N.

Лемма доказана.

Для пары пространств определим интерполяционные пространства аналогично [5] .

Пусть , тогда

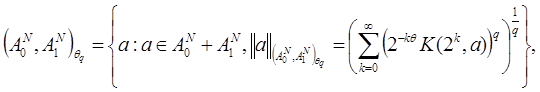
где

При q=∞

Лемма 4.4 Пусть , d>1. Тогда

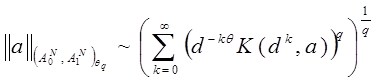
Справедлива следующая

Теорема 4.1 Пусть ≤p0<p1<∞, 1<q0,q1≤∞, M – произвольная сеть. Тогда

↪

где

Доказательство.

Учитывая, что ↪нам достаточно, доказать следующее вложение

↪

Пусть Рассмотрим произвольное представление a=a0+a1, где

тогда

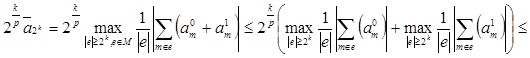
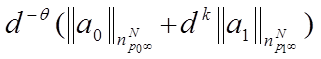(3)

Так как представление a=a0+a1 произвольно, то из (3) следует

Где Рассматривая норму элемента в пространстве и применяя

лемму 4.4 , получаем:

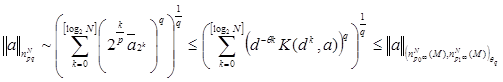
Теорема доказана.

Теорема 4.2 Пусть 1≤p0<p1<∞, 1<q0,q1≤∞, Тогда имеет место равенство

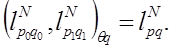
Это равенство понимается в смысле эквивалентности норм с константами, не зависящими N.

Доказательство. По теореме 4.1 и того, что является обобщением пространств Лоренца нам достаточно доказать следующее вложение:

↩

.

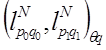Определим элементы и следующим образом

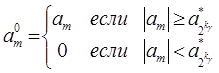
, тогда .

Заметим что

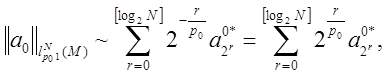(4)

где

(5)

где

Тогда

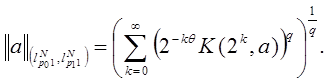
Из (4) и (5) имеем:

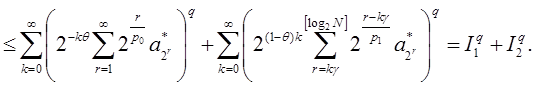
Оценим отдельно каждое из слагаемых последнего равенства, используя неравенство Гельдера:

~

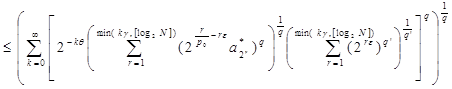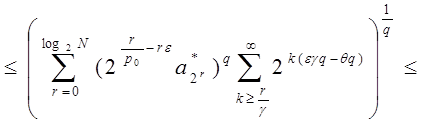
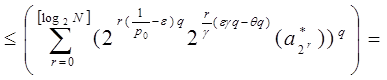
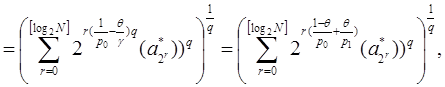
где .

Таким образом, получаем, что Аналогично рассмотрим второе слагаемое:

~

~

~

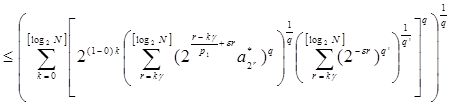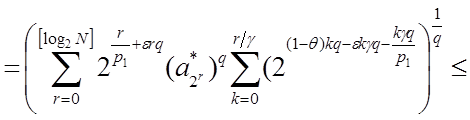
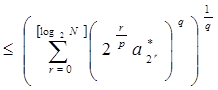Таким образом, получаем

где c не зависит от .

Теорема доказана.

Теорема 4.3 Пусть - матрица , тогда

~

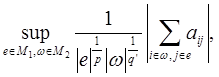
Причем соответствующие константы не зависят от

Доказательство.

Воспользуемся эквивалентными представлением нормы и неравенством о перестановках, получим

 Скачать реферат