Некоторые интерполяционные свойства конечномерных сетевых пространств и пространств Лоренца

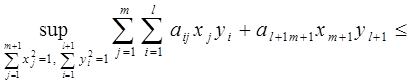
где элемент имеет координаты (l,m).

Теорема доказана. Аналогичные задачи для интегральных операторов были рассмотрены в

работах [1], [5].

4. Некоторые интерполяционные свойства семейств конечномерных пространств

Пусть 1 ≤ p < ∞, 1 ≤ q ≤ ∞. Определим семейство конечномерных пространств:

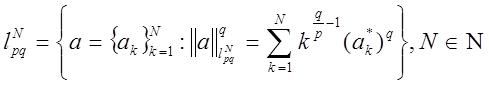
где невозрастающая перестановка последовательности . Обозначим через –множество всех непустых подмножеств из {1,2, .N} Пусть M, 1 ≤ p < ∞, 1 ≤ q ≤ ∞, множество M назовем сетью.

Определим семейство конечномерных пространств

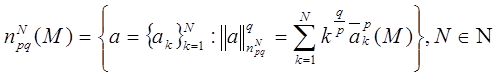
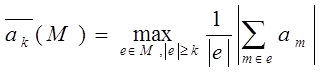
|e| - количество элементов множества e.

При q=∞ положим

Данные пространства являются конечномерными аналогами сетевых пространств, введенных в [1].

Будем говорить что {AN} ↪ {BN} если существует константа c, такая что для любого , где c не зависит от .

Лемма 4.1 Пусть 1 ≤ q <q1≤ ∞, 1 ≤ p ≤ ∞, . Тогда имеет место вложение

↪

то есть

где с не зависит от выбора N.

Доказательство. Пусть

(1)

то есть ↪

Теперь рассмотрим случай, когда 1 ≤ q <q1< ∞, и воспользуемся неравенством (1)

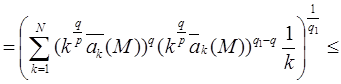
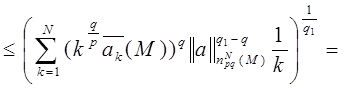
Лемма доказана.

Лемма 4.2 Пусть 1≤p<p1<∞, 1≤q,q1≤∞. Тогда имеем место вложение

↪

Доказательство.

Согласно условию леммы, нам достаточно доказать вложения при p < p1 :

↪

Получаем:

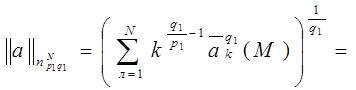
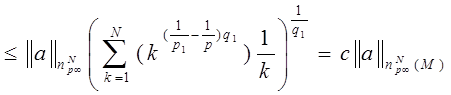
Лемма доказана.

Лемма 4.3 Пусть 1<p<∞, 1≤q≤∞, M= . Тогда

Равенства понимаются с точностью до эквивалентности норм, причем константы не зависят от.

Доказательство. Сначала докажем соотношение:

(2)

Заметим, что

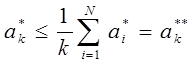
Поэтому

Теперь покажем обратное неравенство. Пусть . Учитывая выбор имеем.

~

~

Заметим, что

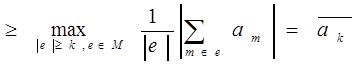
Согласно (2) получаем:

то есть ↪.

Докажем обратное включение. Пусть Введем следующие обозначения:

Тогда

.

Пусть для определенности

.

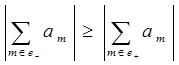Возможны следующие случаи:

.

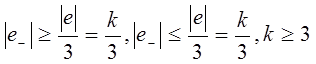В первом случае получаем, что

.

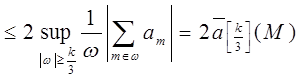Во втором случае , следовательно . Представим , тогда . Здесь и далее - целая часть числа .

Получаем

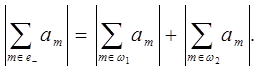
Заметим, что существует такое, что

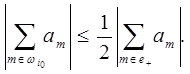
Положим Тогда .

 Скачать реферат