Линейные и нелинейные электрические цепи постоянного тока
На схеме искомый ток I2 определим по закону Ома для замкнутой цепи: ![]() , где Eэ - ЭДС эквивалентного генератора, ее величину определяют как напряжение на зажимах генератора в режиме холостого хода, Eэ=Uxx - внутреннее сопротивление эквивалентного генератора, его величина рассчитывается как эквивалентное сопротивление пассив
, где Eэ - ЭДС эквивалентного генератора, ее величину определяют как напряжение на зажимах генератора в режиме холостого хода, Eэ=Uxx - внутреннее сопротивление эквивалентного генератора, его величина рассчитывается как эквивалентное сопротивление пассив
ного двухполюсника относительно исследуемых зажимов. Изображаем схему эквивалентного генератора в режиме холостого хода (рис.1.5), т.е. при отключенном потребителе R2 от зажимов а и б. В этой схеме есть контур, в котором течет ток режима холостого хода.
Определим его величину:
![]() А.
А.
Зная Ixx величины сопротивлений и ЭДС, в схеме можно определить Uxx как разность потенциалов между клеммами а и б. Для этого потенциал точки а будем считать известным и вычислим потенциал точки б.
φб=φа+E2-IxxּR5 тогда Uxx=φб-φа=E2-IxxּR5=30-0,141ּ52=22,668В
Для расчета внутреннего сопротивления эквивалентного генератора необходимо преобразовать активный двухполюсник в пассивный (рис.1.6), при этом ЭДС Е1 и E2 из схемы исключается, а внутренние сопротивления этих источников r01 и r02 в схеме остаются.
Вычисляем эквивалентное сопротивление схемы (рис 1.6) относительно зажимов а и б:
|
рис 1.6 |
Зная ЭДС и внутреннее сопротивление эквивалентного генератора, вычисляем ток в исследуемой ветви:
|
7) Построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.
Возьмем контур ABFE. Зададимся обходом контура против часовой стрелке. Заземлим одну из точек контура, пусть это будет точка А. Потенциал этой точки равен нулю, φA=0 (рис.1.1). Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу. Начнем обход от точки А.
φA’=φA+E1-I1r01=0+20-0,313ּ1=19,687 В
φB=φA’-I1R1=19,687-0,313ּ64=-0,345 В
φF=φB-I3R4= - 0,345-0,32ּ25=-8,345 В
φF’=φF-I4R2=-8,345-0,481ּ43=-29,028 В
φE=φA=φF’+E2-I4r02= - 29,028+30-0,481ּ2=0 В
Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивления контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат - потенциалы точек с учетом их знака.
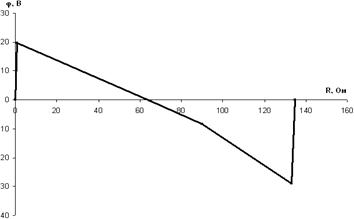
рис.1.7
1.2 Расчет нелинейных электрических цепей постоянного тока
Построить входную вольтамперную характеристику схемы (рис.1.8) Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные вольтамперные характеристики.
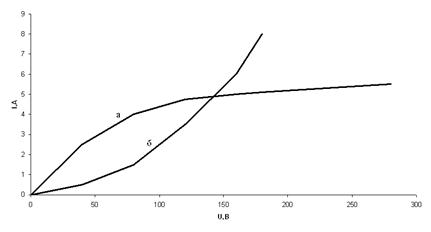
Использовать вольтамперные характеристики элементов "а" и "б" (рис 1.9).
|
рис 1.8 |
| ||
|
рис 1.9 | |||
Расчет цепи производим графическим методом. Для этого в обшей системе координат строим вольтамперные характеристики (ВАХ) линейного и нелинейных элементов: I1=f (U1), I2=f (U2), I3=f (U3) (рис 1.10).
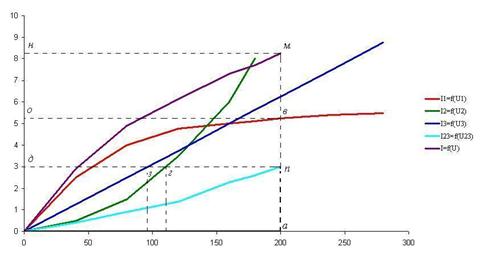
рис 1.10
ВАХ линейного элемента строим по уравнению ![]() . Она представляет собой прямую, проходящую через начало координат.д.ля определения координаты второй точки ВАХ линейного элемента задаемся произвольным значением напряжения. Например, UR=160В, тогда соответствующее значение тока
. Она представляет собой прямую, проходящую через начало координат.д.ля определения координаты второй точки ВАХ линейного элемента задаемся произвольным значением напряжения. Например, UR=160В, тогда соответствующее значение тока ![]() А. Соединив полученную точку с началом координат, получим ВАХ линейного элемента.
А. Соединив полученную точку с началом координат, получим ВАХ линейного элемента.
Далее строится общую ВАХ цепи с учетом схемы соединения элементов. В нашей цепи соединение элементов смешанное. Поэтому графически "сворачиваем" цепь. Начнем с элемента I1=f (U1) (нэ1), он подсоединен параллельно цепи и его ВАХ будет таким же, как и при дано. Далее делаем характеристики линейного элемента I3=f (U3) и нелинейного элемента (нэ2) I2=f (U2), которые соединены между собой последовательно. Строим для них общую ВАХ. В данном случае задаемся током и складываем напряжения. Проделываем это многократно. По полученным точкам строим общую ВАХ цепи I23=f (U23). Затем строим ВАХ нелинейного элемента I1=f (U1) и I23=f (U23), они подсоединены в цепи параллельно, значит, их ток будет равен сумме токов I1=f (U1) и I23=f (U23), значит складываем на графике их общий ток I=f (U).
Дальнейший расчет цепи производим по полученным графикам.
Чтобы найти токи и напряжение на всех элементах цепи поступим так: по оси напряжение находим напряжение равное 200 В (точка а). Из этой точки восстанавливаем перпендикуляр до пересечения I1=f (U1), получаем точку "в". Из точки "в" опустим перпендикуляр на ось тока и получим точку "о", и получим ток (нэ1). Iнэ1=5,2А. Так же восстановим перпендикуляр из точки "а" до пересечение I23=f (U23) и опустим его на ось тока, получим ток во второй ветви I3, не2=I3=Iне2=3А. Отрезке "нд" пересекает ВАХ I3=f (U3) и I2=f (U2) в точках "з" и "г", опустим там перпендикуляры мы получим напряжение на элементах R3 (U3=95В) и (нэ2) (Uнэ2=105В).
2. Анализ электрического состояния линейных электрических цепей переменного тока: однофазных, трехфазных. Исследование переходных процессов в электрических цепях
2.1 Расчет однофазных линейных электрических цепей переменного тока
К зажимам электрической цепи (рис 2.1), подключен синусоидальное напряжение u=54sin (ωt+60º) В частотой f=50Гц.
Выполнить следующее:
определить реактивное сопротивление элементов цепи;
определить действующие значения токов во всех ветвях цепи;
записать уравнение мгновенного значения тока источника;
составить баланс активных и реактивных мощностей;
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода


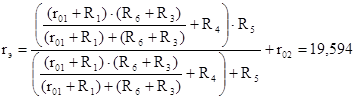 Ом
Ом