Линейные и нелинейные электрические цепи постоянного тока

построить векторную диаграмму токов, совместимую с топографической векторной диаграммой напряжений.

1) Реактивное сопротивление элементов цепи.

Ом,

Ом,

Ом,

Ом.

2) Расчет токов в ветвях цепи выполнен методом эквивалентных преобразований.

Представим схему, приведенную на рисунке 2.1, в виде:

рис 2.2

Находим комплексные сопротивления ветвей, затем участков цепи и всей цепи:

Ом; Ом;

Ом;

Ом;

Ом;

Ом.

Выразим действительное значение напряжение в комплексной форме:

В.

Вычисляем общий ток цепи:

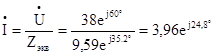А.

Для определения токов параллельных ветвей I1, I2, I3, рассчитываем напряжение на зажимах:

В

Вычисляем токи ветвей:

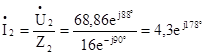А;

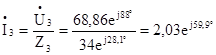А;

А.

3) Уравнение мгновенного значения тока источника:

;

А.

4) Составить баланс активных и реактивных мощностей:

где Sист=150,488 ВּА,

Pист=122,96 Вт,

Qист= - 86,74 вар.

Активная Pпр и реактивная Qпр мощность приемников:

Pпр=I32 (R1+R2) =2,032ּ30=123,62 Вт;

Qпр=I12 (XL1) +I22 (-XC2) +I32 (XL2) +I42 (-XC1) =6,892ּ10+4,32ּ (-16) +2,032ּ16+3,962ּ (-10) =-88вар

Баланс мощностей выполняется:

Pист=Pпр, Qист=Qпр

123Вт=124Вт, - 87вар=-88вар.

Баланс мощностей практически сходится.

5) Напряжения на элементах:

6) Строим топографическую векторную диаграмму на комплексной плоскости.

Выбираем масштаб: MI=1 А/см, MU=10 В/см.

Определяем длины векторов токов и напряжений:

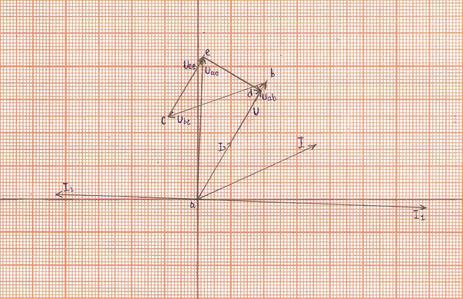
рис 2.3

На комплексной плоскости в масштабе откладываем векторы токов в соответствии с расчетными значениями, при этом положительные фазовые углы отсчитываем от оси (+1) против часовой стрелке, а отрицательные - по часовой стрелке.

Топографическая векторная диаграмма напряжений характерна тем, что каждой точке диаграммы соответствует определенная точка электрической цепи. Построение векторов напряжений ведем, соблюдая порядок расположения элементов цепи и ориентируя векторы напряжений относительно векторов тока: на активном сопротивлении ток и напряжение совпадают по фазе, на индуктивном элементе напряжение опережает ток на 90°, а на емкостном напряжение отстает от тока на 90°.

2.2 Расчет трехфазной линейной цепи переменного тока

В цепи, изображенной на схеме (рис.2.4), потребители соединены треугольником. Известно линейное напряжение Uл=38 В и сопротивление фаз. RAB=18,8 Ом; RBC=3,8 Ом; RCA=3,1 Ом; XLAB=0,68 Ом; XLAC=2,57 Ом; XCBC=2,2 Ом.

Определить фазные, линейные токи, мощности активные, реактивные, полные мощности каждой фазы и всей цепи. Построить векторную диаграмму цепи.

 Скачать реферат