Линейные и нелинейные электрические цепи постоянного тока

При соединении трехфазной цепи треугольником расчет будет вести символическим методом.

1) Модули фазных напряжений при соединении треугольником равны линейным напряжениям.

UЛ=UФ=38 В, то есть В

Комплексы данных напряжений запишем из условия, что вектор совмещен с действующей осью комплексной плоскости;

В;

В;

В.

2) Вычислить комплексы фазных сопротивлений.

Ом,

где ZAB=2 Ом, φAB=19,9º;

Ом,

где ZBC=4,82 Ом, φBC=30º;

Ом,

где ZCA=4,03 Ом, φCA=39,5º.

3) Определить фазные токи:

А,

модуль IAB=19 А, ψAB=-19,9º;

,

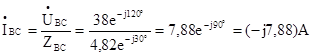модуль IBC=7,88 А, ψBC=-90º;

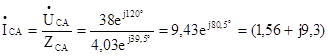А,

модуль ICA=9,43 А, ψCA=80,5º.

4) Находим линейные токи из уравнений, записанных по первому закону Кирхгофа для узлов A, B, C.

А,

модуль IА=22,69 А, аргумент ψА=44º;

А,

модуль IB=17,93 А, аргумент ψB=-4,5º;

A,

модуль IC=17,25 А, аргумент ψC=84,9º.

5) Вычислить мощность каждой фазы и всей цепи:

ВּА,

где SAB=722 BּA, PAB=679,89 Вт, QAB=-245,75 вар;

ВּА,

где SВС=299,44 BּA, PBС=-259,32 Вт, QAB=149,72 вар;

ВּА,

где SCA=360,24 BּA, PCA=-337,43 Вт, QAB=-126,16 вар;

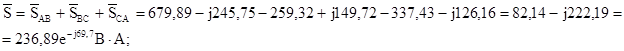где S=236,89 BּA, P=82,14 Вт, QAB=-222,19 вар.

6) Строим в масштабе векторную диаграмму напряжений и токов.

Векторы фазных токов , , строятся под углами ψAB, ψBC, ψCA к действительной оси. К концам векторов , , пристраиваются отрицательные фазные токи согласно уравнениям:

, , .

Замыкающие векторные треугольники векторов , , представляют в выбранном масштабе линейные токи.

Выбираем масштаб: MI=3 А/см.

см;

см;

см.

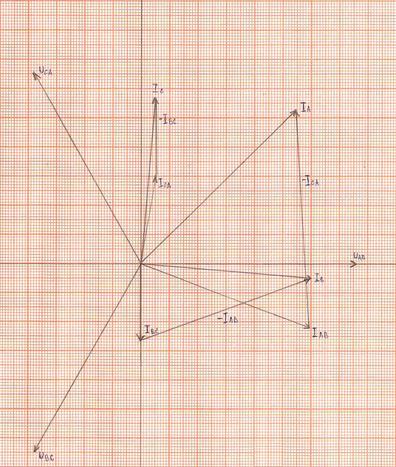
рис 2.5

2.3 Исследование переходных процессов в электрических цепях, содержащих конденсатор и сопротивление

Цепь с последовательно включенными конденсатором емкостью С = 50 мкФ и сопротивлением R = 10 КОм подсоединяется к источнику постоянного напряжения U = 50 В (переключатель в положении 1). Определить законы изменения переходных напряжений и тока при заряде конденсатора и построить их графики. Затем цепь отключается от источника и одновременно переключатель переводится в положение 2. Определить законы изменения переходных напряжений и тока при разряде конденсатора и построить их графики. Определить фактическую длительность заряда и разряда конденсатора и энергию электрического поля при 1 = Зτ. Схема цепи приведена на рис.2.6

1) Переключатель в положении 1 (заряд конденсатора)

τ =RּC=104ּ50ּ16-6=0,5c

На основании второго закона коммутации получены законы, характеризующие напряжение и ток при заряде конденсатора.

где U - напряжение источника

uуст=U - установившееся значение напряжения при заряде конденсатора

- свободная составляющая напряжения при заряде конденсатора.

Зарядный ток равен свободной составляющей, т.к ток установившегося режима равен 0 (iуст=0).

Длительность заряда конденсатора:

t=5τ=5ּ0,5=2,5 с.

Вычисляем значение напряжения на конденсаторе при его заряде для значений времени t=0, τ, 2τ, 3τ, 4τ, 5τ.

t=0, В;

t=τ, B;

t=2τ, B;

t=3τ, B;

t=4τ, B;

t=5τ, B.

Аналогично вычисляем значения зарядного тока согласно закону изменения переходного тока при заряде конденсатора для значений времени t=0, τ, 2τ, 3τ, 4τ, 5τ.

 Скачать реферат