Рассчет изменения скорости химической реакции

Рефераты / Химия / Рассчет изменения скорости химической реакции

Системы, в которых энергетическое взаимодействие между дисперсной фазой и дисперсионной средой проявляется слабо (например, частицы металлов или галогенидов серебра в воде) называются лиофобными (или в водной среде – гидрофобными, т.е. не любящими воду). Если же в дисперсной системе интенсивность молекулярных взаимодействий на границе раздела фаз является сильно выраженной (например, в раствора

х ВМС, белков), то такие системы называются лиофильными (или в водной дисперсионной среде – гидрофильными, т.е. любящими воду). Коллоидными свойствами могут обладать системы и с неорганическими, и с органическими фазовыми компонентами. К дисперсным системам относятся как разнообразные природные объекты, так и многочисленные продукты их переработки, причем дисперсная фаза в них, как правило, полидисперсная, т.е. размеры частиц находятся в значительном интервале. Классификация дисперсных систем по агрегатному состоянию дисперсной фазы и дисперсионной среды

Дисперсионная среда	Дисперсная фаза	Название дисперсной системы	Примеры дисперсных систем
Жидкость	Твердое тело	Суспензия, золь	Золи металлов, природные воды
	Жидкость	Эмульсия	Молоко, нефть
	Газ	Пена	Мыльная пена
Твердое тело	Твердое тело	Минерал, сплав	Рубин, сталь
	Жидкость	Пористое тело, минерал	Влажный грунт, опал
	Газ	Пористое тело	Сухой грунт, активированный уголь, пенопласт
Газ	Твердое тело	Аэрозоль	Пыль, дым
Газ	Жидкость	Аэрозоль	Туман, облако

61. Рассчитать средний сдвиг частиц аэрозоля с радиусом частиц 10-7 м за время 10 с при температуре 273 К и вязкости воздуха 1,7·10-5 н·с/м2. Как изменится средний сдвиг частиц, если радиус частиц аэрозоля увеличится до 10-6 м?

Средний сдвиг частиц аэрозоля

t - время, за которое происходит смещение частицы (продолжительность диффузии), с;

D - коэффициент диффузии, м2 . с-1.

Коэффициент диффузии для сферической частицы рассчитывается по уравнению Эйнштейна:

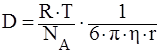где NА – число Авогадро, 6 · 10 23 молекул/моль;

h – вязкость дисперсионной среды, Н · с/м2 (Па · с);

r – радиус частицы, м;

R – универсальная газовая постоянная, 8,314 Дж/моль · К;

T – абсолютная температура, К;

p - число 3,14.

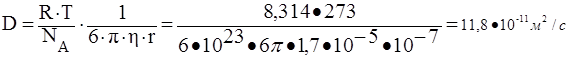
ответ на второй вопрос задания:

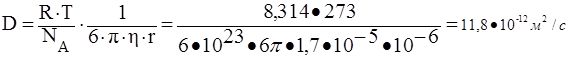
Таким образом, средний сдвиг частицы уменьшиться в 10 раз.

Ответ: , уменьшится в 10 раз.

79. Объяснить причины, по которым определение количества адсорбирующегося вещества и описание адсорбционных явлений проводят с использованием нескольких теорий и уравнений: Гиббса, Ленгмюра, Фрейндлиха и др. В чем их особенности?

На границе раздела фаз, например жидкости и воздуха, молекулы вещества в глубине одной из фаз и на ее поверхности энергетически неравноценны. На молекулу внутри фазы со всех сторон действуют межмолекулярные силы, уравновешивающие друг друга. А на поверхностную молекулу со стороны дисперсной фазы, с одной стороны, и дисперсионной среды – с другой – действуют силы, разные по величине. Таким образом, на поверхности дисперсных частиц появляется избыточная энергия. Такая картина характерна для любых поверхностей раздела фаз. Чем больше поверхность раздела, тем больше накопленная поверхностная энергия в межфазном поверхностном слое. Это является причиной неустойчивости системы, поскольку в ней самопроизвольно могут протекать процессы, направленные всегда на снижение поверхностной энергии путем уменьшения величины удельной поверхности (например, капля жидкости всегда стремится принять форму шара, поскольку шар обладает минимальной площадью поверхности).

Величина поверхностной энергии определяется уравнением

F = s ·S,

где F – свободная поверхностная энергия, Дж;

s – величина поверхностного натяжения, Дж/м2;

S – поверхность дисперсных частиц (площадь поверхности раздела), м 2.

Самопроизвольные процессы, идущие с уменьшением площади поверхности S, называются коагуляцией, а процессы, идущие с уменьшением s, в частности при увеличении концентрации вещества в поверхностном слое по сравнению с концентрацией его в объеме фазы, называются адсорбцией.

Адсорбция – процесс самопроизвольного поглощения вещества (адсорбтива) поверхностью адсорбента. Уравнение Гиббса устанавливает взаимосвязь величины адсорбции (Г, кмоль/кг или кмоль/м 2) с изменением поверхностного натяжения (s, Дж/м2 ) от концентрации раствора (С, кмоль/л).

где С – концентрация раствора, кмоль/л;

R – универсальная газовая постоянная;

T – температура;

ds /dС – производная, являющаяся мерой поверхностной активности; может быть определена графически по зависимости поверхностного натяжения от концентрации (при s®0).

Физические процессы молекулярной адсорбции на твердой поверхности описываются уравнениями Ленгмюра и Фрейндлиха.

Уравнение Ленгмюра: