Динамическое программирование

В настоящее время известно большое количество модификаций системы сетевого планирования и управления: RAMPS, PERT, CRM, LESS, COMET и ряд других.

В свое время в СССР также была разработана система сетевого планирования и управления (СПУ), включающая методы КОППР,СУР, КОМПАС и другие. Система СПУ основана на использовании современных достижений в области общей теории управления, кибернетики

прикладной математики и вычислительной техники.

В сетевом планировании и управлении широко применяется аппарат математического программирования, теории графов, теория вероятностей и других математических дисциплин. Формализация задач планирования и управления позволяет широко использовать средства вычислительной техники и строить сетевые системы по общим принципам построения АСУ.

Предпосылкой создания сетевых систем являлось развитие раздела исследования операций, изучающего модели упорядочивания. Идея моделирования комплексов операций с помощью сетей привела к появления самостоятельного направления в теории и практике организационного управления, получившего в отечественной литературе название сетевого планирования и управления (СПУ).

Все методы сетевого планирования имеют в своей основе сетевую модель, в которой условными знаками – стрелками изображают во взаимосвязи работы, которые необходимо выполнить для достижения поставленной цели. Сеть может быть укрупненной или детальной, но в любом случаи она должна давать представление о том, какими путями можно прийти к коночной цели и какие издержки при этом потребуются. Уже одно то, что информация о предполагаемом ходе выполнения работ представляется в виде сети, наглядно изображающей условия выполнения каждой из работ в общем комплексе, является достаточной рекомендацией к использованию сетевых графиков в практической работе. При вычерчивании сети легко выявляются все недостатки, логические неувязки в организационной структуре планируемого мероприятия.

Графическое изображение планов в виде сети позволяет охватить весь комплекс в целом и сосредоточится на отдельных участках. Обзорность и полнота информации, представленный графически, сочетаются с доступностью её для понимания специалистами, в то время как словесное описание всегда дается в расчете лишь на определенный круг работников.

Помимо графического изображения работ, которые предполагается выполнить для достижения намеченной цели, сетевой график содержит некоторые оценки (времени, стоимости, ресурсов, технической надежности элементов), даваемые каждой работе в отдельности. Эти оценки могут быть точными или приближенными. С известной вероятностью появления каждой из них. Сетевой график с нанесенными на него оценками служит основой для последующего анализа возможных изменений и контроля за его выполнением. Основными параметрами, которые оцениваются при таком анализе, служат время и затраты. Эти два фактора, как правило, находятся в непосредственной зависимости один от другого: чем короче заданный срок выполнения работ, тем больше затрат потребуется на их выполнение, и наоборот. Анализ сетевого графика в системе СПУ позволяет выбрать оптимальный вариант плана, обеспечивающий выполнение всех работ в заданные сроки с минимальными затратами. Система СПУ предусматривает либо одну оценку времени для выполнения каждой работы – «наиболее вероятное время», либо три оценки: «оптимистическую», «пессимистическую» и «наиболее вероятную» оценки времени по каждой работе. Эти три оценки используются для расчета среднего ожидаемого времени выполнения работ и вычисления вероятности выполнения программы в заданные сроки. Несмотря на указанные и некоторые другие различия в методах анализа сетевых моделей, общая их идея одна – все они используют графическое построение в виде сети с временными или другими оценками для планирования действий, приводящих в конечном итоге к желаемому результату. (5)

III Практическое применение динамического программирования

Задача о выборе наиболее экономного маршрута доставки груза.

На данной сети дорог имеется несколько маршрутов, по которым можно доставлять груз из пункта 1 в пункт 10 (рис. 1). Известны стоимости перевозки единицы груза между отдельными промежуточными пунктами сети (они проставлены на сети у соответствующих ребер). Требуется в системе дорог выбрать маршрут доставки груза из пункта 1 в пункт 10, которому соответствует наименьшие затраты.

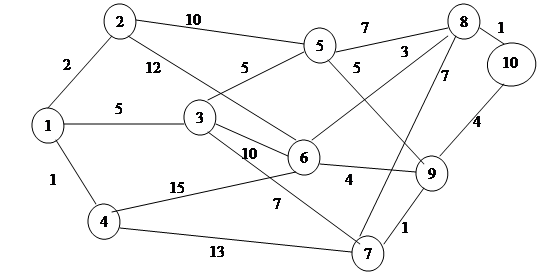
рис. 1

Для решения задачи методом динамического программирования разобьем все пункты сети на группы (табл. 1).

Таблица 1

К группе I отнесем пункт 1, к группе II – пункты, в которые можно попасть из пункта 1 (таковыми будут 2; 3; 4), к группе III отнесем пункты, в которые можно попасть непосредственно из любого пункта группы II (таковыми будут 5; 6; 7), и т.д. в результате движение транспорта с грузом из пункта 1 в пункт 10 примет поэтапный характер: на первом этапе транспорт перемещается из пункта 1 в какой-то пункт группы II, на втором этапе – из пункта группы II в пункт группы III и т.д. Вместе с этим и процесс нахождения наиболее экономного маршрута из пункта 1 в пункт 10 распадается на шаги. На каждом шаге надо так выбрать маршрут следования груза в пункт соседней группы, чтобы доставка груза по всему маршруту была сопряжена с минимальными затратами. Избранный нами подход к решению задачи учитывает особенности сети, изображенной на рис. 1: после разбиения на группы пункты, оказавшиеся в одной и той же группе, дорогами не соединены.

Применительно к рассматриваемой задаче принцип оптимальности можно сформулировать так: оптимальный маршрут доставки груза из пункта 1 в пункт 10 обладает тем свойством, что, каков бы ни был маршрут достижения некоторого промежуточного пункта сети, дальнейший маршрут следования должен совпадать с оптимальным маршрутом для части маршрута, начинающейся с этого пункта.

В данном случае процесс состоит из четырех шагов (рис. 2). Будем оптимизировать каждый шаг, начиная с последнего – четвертого. На этом шаге в пункт 10 можно попасть из пункта 8 или 9, причем из каждого пункта только одним способом. Если предпоследний, третий, шаг привел груз в пункт 8, то дальше следует двигаться по маршруту 8 – 10, и затраты на перевозку единицы груза будут равны единице; если же в пункт 9 – то следует двигаться по маршруту 9 – 10, на котором затраты составят 4 единицы. Условное оптимальное решение помечаем на сети стрелкой, выходящей из соответствующего кружка, а величину затрат записываем в нижней половинке кружка.

 Скачать реферат