Радиотехническая система передач

как можно дальше друг от друга. Из этой же – мерной модели следует геометрическая интерпретация расстояния Хэмминга: – это число рёбер, которые нужно пройти, чтобы перевести один вектор в другой, т.е. попасть из вершины одного вектора в вершину другого.

2.1 Обнаружение и исправление ошибок

Стратегия обнаружения заключается в следующем. Декодер обнаруживает ошибку при априорном условии, что переданным словом было ближайшее по расстоянию к принятому слову. Покажем применение этого утверждения.

Пример 1. Пусть ; . Разрешенным для передачи является множество кодовых слов:

.

Очевидно, что код имеет . Любая одиночная ошибка трансформирует данное кодовое слово в другое разрешенное слово. Это случай безизбыточного кода, не обладающего корректирующей возможностью.

Пример 2. Пусть теперь подмножество разрешённых кодовых слов предоставлено в виде двоичных комбинаций с чётным числом единиц.

.

Заданный код имеет . Запрещенные кодовые слова представлены в виде подмножества :

.

Если , то ни одно из разрешенных кодовых слов (т.е. кода ) при одиночной ошибке не переходит в другое разрешённое слово этого же кода. Таким образом, код обнаруживает:

– одиночные ошибки;

– ошибки нечетной кратности (для - тройные).

Например, тройная ошибка кодового слова ; , переводит его в запрещенный вектор .

Вывод – В общем случае, при необходимости обнаруживать ошибки кратности кодовое расстояние кода должно быть

.

Пример 3. Пусть ; ; код задан векторами и .

При возникновении одиночных ошибок или множества векторов

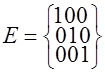
кодовому слову соответствует следующее запрещенное подмножество

==

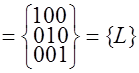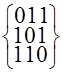Таким образом, коду – разрешенному для передачи подмножеств векторов соответствует два запрещенных подмножества векторов и :

=

= .

=

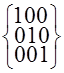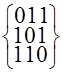Стратегия исправления ошибок заключается в следующем:

– каждая из одиночных ошибок приводит к запрещенному кодовому слову того или иного запрещенного подмножества (и );

– структура кодового запрещенного подмножества, относящаяся к соответствующему исходному разрешенному подмножеству, позволяет определить местоположение ошибки, т.е. исправить ошибку.

Для исправления ошибок кратности кодовое расстояние должно удовлетворять соотношению . (1.2)

Используя эту формулу, можно записать

,

где обозначает целую часть числа .

Замечание – Существуют модели каналов (например, канал с дефектами), в которых величина может быть больше, чем в выражении (1.2).

ЛИТЕРАТУРА

· Митюхин А.И., Игнатович В.Г. Линейные групповые коды: Учеб. пособие. – Мн. :БГУИР, 2002.

· Митюхин А.И. Элементы абстрактной алгебры: Учеб.пособие. – Мн.: БГУИР, 2000.

 Скачать реферат