Моделирование голограммы, получаемой с помощью подповерхностного сканирующего радиолокатора

.

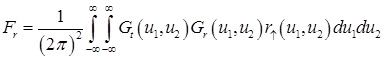В полученном выражении комплексное число , как и следовало ожидать, не зависит от координат центра апертуры. Величина зависит от комплексной диэлектрической проницаемости нижнего полупространства че

рез коэффициент отражения Френеля и является постоянным слагаемым, которое, наряду с опорным сигналом от передатчика к приемнику, добавляется к сигналу, регистрируемому радиолокатором после отражения от рассеивателей, находящихся в нижнем полупространстве.

Коэффициенты прохождения и отражения Френеля для плоской волны

Найдем коэффициенты Френеля для отражения и прохождения плоской волны, задаваемой уравнением

,

в котором величины , и в общем случае могут быть комплексными и не иметь смысла проекций волнового вектора на оси координат. В таком случае уравнение будет описывать как однородную, так и неоднородную волну, в которой направление убывания амплитуды и направление распространения могут не совпадать [10]. Подстановка в уравнение Гельмгольца, записанного для однородной среды вне области, занятой источниками

,

в котором

,

позволяет получить условие, которое должно выполняться для величин , и в общем случае

.

В предыдущих параграфах, плоская волна и соответствующие ей коэффициенты отражения и преломления характеризовались парой чисел и , а не с помощью угла падения или скольжения, поскольку для удобства последующих расчетов, с применением быстрого алгоритма преобразования Фурье, удобно поступить именно так. Найдем соответствующие коэффициенты отражения и преломления как функции и , т.е. именно в таком виде, в котором они фигурируют в формулах из предыдущих параграфов.

Рис. 2. К выводу френелевских коэффициентов отражения и прохождения для однородных и неоднородных плоских волн.

Пусть на поверхность раздела падает плоская волна, задаваемая уравнением (рис. 2). Решение задачи будем искать в виде трех волн: падающей и отраженной в верхнем полупространстве и преломленной в нижнем полупространстве, причем отраженную и преломленную плоские волны запишем в виде

,

.

В формулах и векторы , в общем случае являются комплексными.

На границе раздела двух сред должны удовлетворяться граничные условия [10]

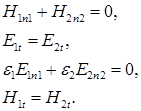
В выражении для граничных условий первый встречающийся индекс обозначает среду: 1 – верхнее полупространство, 2 – нижнее; индекс , – обозначают проекцию на нормаль, проведенную в верхнюю и нижнюю среду соответственно; индекс – обозначает проекцию на касательный к границе раздела вектор.

Для комплексных амплитуд горизонтальной поляризации отраженной и прошедшей волн получаются следующие выражения

,

,

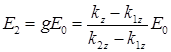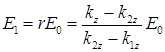в которых – компоненты комплексного волнового вектора в каждой среде связаны с и соотношениями аналогичными . Индекс при этом обозначает третью компоненту в соответствующей среде. Таким образом, могут быть получены следующие формулы для коэффициентов прохождения и отражения для любого типа плоских волн

,

,

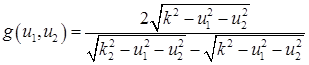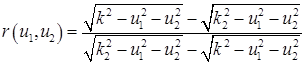в которых знаки перед корнями должны выбираться с учетом требуемых проекций – компонент волновых векторов на оси координат.

Радиоголограмма точечного источника

В качестве примера рассчитаем с использованием приведенных выше формул голограмму точечного рассеивателя, находящегося в нижнем полупространстве. Предположим, что в качестве сигнала, регистрируемого радиолокатором, будет являться модуль суммы отраженных сигналов от точечного рассеивателя, находящегося под поверхностью, поверхности и некоторого постоянного опорного сигнала, подаваемого непосредственно из передатчика в приемник. Таким образом, голограммой будем называть модуль суммы

,

где введены обозначения , . В выражении задается , а – комплексная величина опорного сигнала.

Так как выбор опорного сигнала допускает некоторый произвол, то сумма сигнала отраженного от поверхности и опорного может принимать любое значение. Для следующего примера в качестве опорного сигнала выбиралось действительное число, равное максимуму модуля сигнала, отраженного от точечного источника. Получившаяся в результате моделирования голограмма изображена на рис. 3.

На осях координат отложено смещение центра апертуры радиолокатора от проекции точечного рассеивателя на поверхность . Величины используемых при расчете голограммы параметров приводятся в таблице 1.

Таблица 1. Величины параметров модели, используемых при моделировании голограммы

 Скачать реферат